


Next: Angle of Contact
Up: Surface Tension
Previous: Spherical Interfaces
Capillary Length
Consider an interface separating the atmosphere from a liquid of uniform density 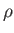 that is at rest on the surface of the
Earth. Neglecting the density of air compared to that of the liquid, the pressure in the atmosphere can
be regarded as constant. On the other hand, the pressure in the liquid varies as
that is at rest on the surface of the
Earth. Neglecting the density of air compared to that of the liquid, the pressure in the atmosphere can
be regarded as constant. On the other hand, the pressure in the liquid varies as
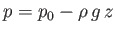 (see Chapter 2), where
(see Chapter 2), where
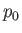 is the pressure of the atmosphere,
is the pressure of the atmosphere, 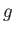 the acceleration due to gravity, and
the acceleration due to gravity, and  measures vertical height (relative
to the equilibrium height of the interface in the absence of surface tension). Note that
measures vertical height (relative
to the equilibrium height of the interface in the absence of surface tension). Note that  increases upward. In this situation, the Young-Laplace equation, (3.12),
yields
increases upward. In this situation, the Young-Laplace equation, (3.12),
yields
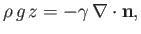 |
(3.15) |
where 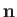 is the normal to the interface directed from liquid to air. If
is the normal to the interface directed from liquid to air. If 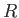 represents the typical radius of curvature of the
interface then the left-hand side of the previous equation dominates the right-hand side whenever
represents the typical radius of curvature of the
interface then the left-hand side of the previous equation dominates the right-hand side whenever 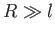 ,
and vice versa. Here,
,
and vice versa. Here,
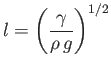 |
(3.16) |
is known as the capillary length, and takes the value
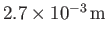 for pure water at
for pure water at
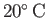 (Batchelor 2000). We conclude that the effect of surface tension on the shape of an liquid/air interface
is likely to dominate the effect of gravity when the interface's radius of curvature is much less than the capillary length, and vice versa.
(Batchelor 2000). We conclude that the effect of surface tension on the shape of an liquid/air interface
is likely to dominate the effect of gravity when the interface's radius of curvature is much less than the capillary length, and vice versa.
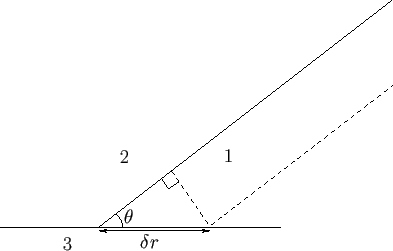
Figure 3.2:
Interface between a liquid (1), a gas (2), and a solid (3).
 |



Next: Angle of Contact
Up: Surface Tension
Previous: Spherical Interfaces
Richard Fitzpatrick
2016-03-31