


Next: Jurin's Law
Up: Surface Tension
Previous: Capillary Length
Suppose that a liquid/air interface is in contact with a solid, as would be the case for water in a glass tube, or a drop
of mercury resting on a table. Figure 3.2 shows a section perpendicular to the edge at which the
liquid, 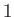 , the air,
, the air, 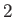 , and the solid,
, and the solid, 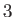 , meet. Suppose that the free energies per unit
area at the liquid/air, liquid/solid, and air/solid interfaces are
, meet. Suppose that the free energies per unit
area at the liquid/air, liquid/solid, and air/solid interfaces are
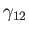 ,
,
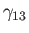 , and
, and
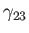 ,
respectively. If the boundary between the three media is slightly modified in the neighborhood of the edge, as indicated
by the dotted line in the figure, then the area of contact of the air with the solid is increased by a small amount
,
respectively. If the boundary between the three media is slightly modified in the neighborhood of the edge, as indicated
by the dotted line in the figure, then the area of contact of the air with the solid is increased by a small amount 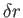 per unit
breadth (perpendicular to the figure), whereas that of the liquid with the solid is decreased by
per unit
breadth (perpendicular to the figure), whereas that of the liquid with the solid is decreased by
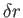 per unit breadth, and that of the liquid with the air is decreased by
per unit breadth, and that of the liquid with the air is decreased by
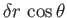 per unit
breadth. Thus, the net change in free energy per unit breadth is
per unit
breadth. Thus, the net change in free energy per unit breadth is
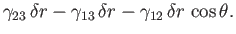 |
(3.17) |
However, an equilibrium state is one which minimizes the free energy, implying that the previous expression is zero for arbitrary
(small) 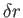 : that is,
: that is,
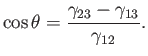 |
(3.18) |
We conclude that, in equilibrium, the angle of contact, 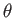 , between the liquid and the solid takes a fixed value that depends on the
free energies per unit area at the liquid/air, liquid/solid, and air/solid interfaces. Note that the previous formula
could also be obtained from the requirement that the various surface tension forces acting at the edge balance one another, assuming that
it is really appropriate to interpret
, between the liquid and the solid takes a fixed value that depends on the
free energies per unit area at the liquid/air, liquid/solid, and air/solid interfaces. Note that the previous formula
could also be obtained from the requirement that the various surface tension forces acting at the edge balance one another, assuming that
it is really appropriate to interpret
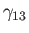 and
and
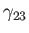 as surface tensions when one of
the media making up the interface is a solid.
as surface tensions when one of
the media making up the interface is a solid.
As explained in Section 3.1, we would generally expect
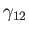 and
and
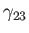 to be positive.
On the other hand,
to be positive.
On the other hand,
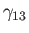 could be either positive or negative. Now, because
could be either positive or negative. Now, because
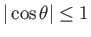 , Equation (3.18)
can only be solved when
, Equation (3.18)
can only be solved when
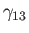 lies in the range
lies in the range
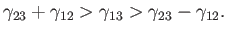 |
(3.19) |
If
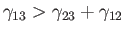 then the angle of contact is
then the angle of contact is 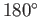 , which corresponds to the case
where the
free energy at the liquid/solid interface is so large that the liquid does not wet the solid at all, but instead breaks up into beads
on its surface. On the other hand, if
, which corresponds to the case
where the
free energy at the liquid/solid interface is so large that the liquid does not wet the solid at all, but instead breaks up into beads
on its surface. On the other hand, if
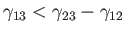 then the
angle of contact is
then the
angle of contact is 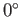 , which corresponds to the case where the free energy at the liquid/solid
interface is so small that the liquid completely wets the solid, spreading out indefinitely until it either covers the
whole surface, or its thickness reaches molecular dimensions.
, which corresponds to the case where the free energy at the liquid/solid
interface is so small that the liquid completely wets the solid, spreading out indefinitely until it either covers the
whole surface, or its thickness reaches molecular dimensions.
The angle of contact between water and glass typically lies in the range 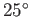 to
to 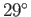 , whereas
that between mercury and glass is about
, whereas
that between mercury and glass is about 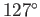 (Batchelor 2000).
(Batchelor 2000).
Figure 3.3:
Elevation of liquid level in a capillary tube.
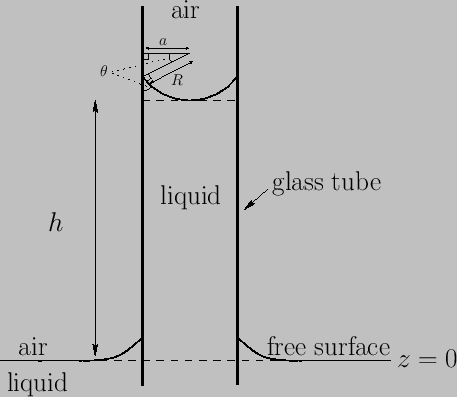 |



Next: Jurin's Law
Up: Surface Tension
Previous: Capillary Length
Richard Fitzpatrick
2016-03-31
![]() and
and
![]() to be positive.
On the other hand,
to be positive.
On the other hand,
![]() could be either positive or negative. Now, because
could be either positive or negative. Now, because
![]() , Equation (3.18)
can only be solved when
, Equation (3.18)
can only be solved when
![]() lies in the range
lies in the range
![]() to
to ![]() , whereas
that between mercury and glass is about
, whereas
that between mercury and glass is about ![]() (Batchelor 2000).
(Batchelor 2000).