 |
Suppose that the body turns through a small angle ![]() about some horizontal axis, lying in the plane
about some horizontal axis, lying in the plane ![]() , that passes through the origin.
Let
, that passes through the origin.
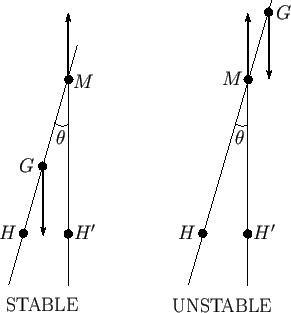
Let ![]() be that, originally vertical, straight-line that passes through the body's center of gravity,
be that, originally vertical, straight-line that passes through the body's center of gravity, ![]() , and
original center of buoyancy,
, and
original center of buoyancy, ![]() . Owing to the altered shape of the volume of displaced water, the
center of buoyancy is shifted to some new position
. Owing to the altered shape of the volume of displaced water, the
center of buoyancy is shifted to some new position ![]() . Let the vertical straight-line
passing through
. Let the vertical straight-line
passing through ![]() meet
meet ![]() at
at ![]() . (See Figure 2.1.) Point
. (See Figure 2.1.) Point ![]() (in the limit
(in the limit
![]() ) is called the metacenter.
In the disturbed state, the body's weight
) is called the metacenter.
In the disturbed state, the body's weight ![]() acts downward through
acts downward through ![]() , and
the buoyancy
, and
the buoyancy
![]() acts upward through
acts upward through ![]() . Let us assume that the submerged volume,
. Let us assume that the submerged volume, ![]() ,
is unchanged from the equilibrium state (which excludes vertical oscillations from consideration). It follows that the weight and
the buoyancy force are equal and opposite, so
that there is no net force on the body. However, as can be seen from Figure 2.1, the weight and the buoyancy force generate a net torque of magnitude
,
is unchanged from the equilibrium state (which excludes vertical oscillations from consideration). It follows that the weight and
the buoyancy force are equal and opposite, so
that there is no net force on the body. However, as can be seen from Figure 2.1, the weight and the buoyancy force generate a net torque of magnitude
![]() . Here,
. Here, ![]() is the length
is the length ![]() : that is, the distance between the metacenter and the
center of gravity. This distance is generally known as the metacentric height, and is defined such that it is
positive when
: that is, the distance between the metacenter and the
center of gravity. This distance is generally known as the metacentric height, and is defined such that it is
positive when ![]() lies above
lies above ![]() , and vice versa.
Moreover, as is also clear from Figure 2.1, when
, and vice versa.
Moreover, as is also clear from Figure 2.1, when ![]() lies above
lies above ![]() the torque acts to reduce
the torque acts to reduce ![]() , and vice versa. In the former case, the torque is known as
a righting torque. We conclude that a floating body is stable to small angular displacements about some horizontal axis lying
in the plane
, and vice versa. In the former case, the torque is known as
a righting torque. We conclude that a floating body is stable to small angular displacements about some horizontal axis lying
in the plane ![]() provided that its metacentric height is positive: that is, provided that the metacenter lies above the
center of gravity. Because we have already demonstrated that a floating body is unconditionally stable to
small vertical displacements (and as it is also fairly obvious that such a body is
neutrally stable to both horizontal displacements and angular displacements about a vertical axis passing through its center of gravity), it follows that a necessary and sufficient condition for the stability
of a floating body to a general small perturbation (made up of arbitrary linear and angular components)
is that its metacentric height be positive for angular displacements about any horizontal axis.
provided that its metacentric height is positive: that is, provided that the metacenter lies above the
center of gravity. Because we have already demonstrated that a floating body is unconditionally stable to
small vertical displacements (and as it is also fairly obvious that such a body is
neutrally stable to both horizontal displacements and angular displacements about a vertical axis passing through its center of gravity), it follows that a necessary and sufficient condition for the stability
of a floating body to a general small perturbation (made up of arbitrary linear and angular components)
is that its metacentric height be positive for angular displacements about any horizontal axis.