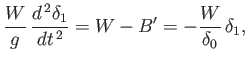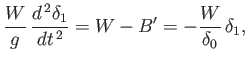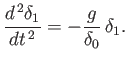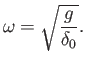Next: Angular Stability of Floating
Up: Hydrostatics
Previous: Equilibrium of Floating Bodies
Consider a floating body of weight 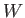 that, in equilibrium, has a submerged volume
that, in equilibrium, has a submerged volume 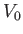 . Thus, the body's downward weight is balanced by the upward buoyancy force,
. Thus, the body's downward weight is balanced by the upward buoyancy force,
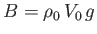 : that is,
: that is,
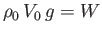 . Let
. Let 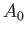 be the cross-sectional area of the body at the waterline (i.e., in the
plane
be the cross-sectional area of the body at the waterline (i.e., in the
plane  ). It is convenient to define the body's mean draft (or mean submerged depth) as
). It is convenient to define the body's mean draft (or mean submerged depth) as
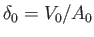 . Suppose that the
body is displaced slightly downward, without rotation, such that its mean draft becomes
. Suppose that the
body is displaced slightly downward, without rotation, such that its mean draft becomes
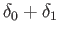 , where
, where
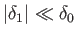 .
Assuming that the
cross-sectional area in the vicinity of the waterline is constant, the new submerged volume is
.
Assuming that the
cross-sectional area in the vicinity of the waterline is constant, the new submerged volume is
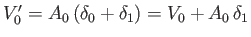 , and the
new buoyancy force becomes
, and the
new buoyancy force becomes
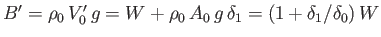 . However, the weight of the body is unchanged. Thus,
the body's perturbed vertical equation of motion is written
. However, the weight of the body is unchanged. Thus,
the body's perturbed vertical equation of motion is written
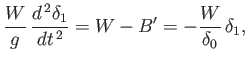 |
(2.19) |
which reduces to the simple harmonic equation
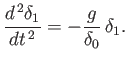 |
(2.20) |
We conclude that if a floating body of mean draft  is subject to a small vertical displacement then it oscillates about its equilibrium position at the
characteristic frequency
is subject to a small vertical displacement then it oscillates about its equilibrium position at the
characteristic frequency
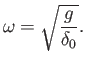 |
(2.21) |
It follows that such a body is unconditionally stable to small vertical displacements. Incidentally, the previous calculation neglects the phenomenon
of added mass, by which some of the water surrounding the floating body oscillates in sympathy with it, thereby increasing the
body's effective inertia. (See Sections 5.9 and 7.10.)



Next: Angular Stability of Floating
Up: Hydrostatics
Previous: Equilibrium of Floating Bodies
Richard Fitzpatrick
2016-03-31