


Next: Tensor Fields
Up: Cartesian Tensors
Previous: Tensors and Tensor Notation
Tensor Transformation
As we saw in Appendix A, scalars and vectors are defined according to their
transformation properties under rotation of the coordinate axes. In fact, a scalar is
invariant under rotation of the coordinate axes. On the other
hand, according to Equations (A.49) and (B.6), the components of a general vector 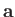 transform under an infinitesimal
rotation of the coordinate axes according to
transform under an infinitesimal
rotation of the coordinate axes according to
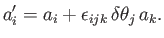 |
(B.24) |
Here, the 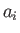 are the components of the vector in the original coordinate system, the
are the components of the vector in the original coordinate system, the 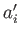 are the
components in the rotated coordinate system, and the latter system is obtained from the former via
a combination of an infinitesimal rotation through an angle
are the
components in the rotated coordinate system, and the latter system is obtained from the former via
a combination of an infinitesimal rotation through an angle
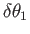 about coordinate axis 1, an infinitesimal rotation through an angle
about coordinate axis 1, an infinitesimal rotation through an angle
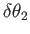 about axis 2, and an infinitesimal rotation through an angle
about axis 2, and an infinitesimal rotation through an angle
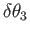 about axis 3. These three rotations can take place in
any order. Incidentally, a finite rotation can be built up out of a great many infinitesimal rotations, so if a vector
transforms properly under an infinitesimal rotation of the coordinate axes then it will also transform properly under a finite rotation.
about axis 3. These three rotations can take place in
any order. Incidentally, a finite rotation can be built up out of a great many infinitesimal rotations, so if a vector
transforms properly under an infinitesimal rotation of the coordinate axes then it will also transform properly under a finite rotation.
Equation (B.24) can also be written
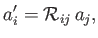 |
(B.25) |
where
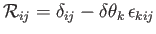 |
(B.26) |
is a rotation matrix (which is not a tensor, because it is specific to the two coordinate systems it transforms
between).
To first order in the
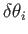 , Equation (B.25) can be inverted to give
, Equation (B.25) can be inverted to give
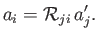 |
(B.27) |
This follows because, to first order in the
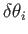 ,
,
where the dummy index 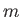 has been relabeled
has been relabeled 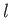 , and use has been made of Equations (B.8), (B.10), and (B.12). Likewise, it is easily demonstrated that
, and use has been made of Equations (B.8), (B.10), and (B.12). Likewise, it is easily demonstrated that
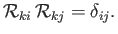 |
(B.29) |
It can also be shown that, to first order in the
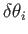 ,
,
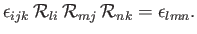 |
(B.30) |
This follows because
Here, there has been much relabeling of dummy indices, and use has been made of Equations (B.10) and (B.16). It can similarly be shown that
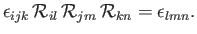 |
(B.32) |
As a direct generalization of Equation (B.25), a second-order tensor transforms under
rotation as
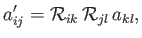 |
(B.33) |
whereas a third-order tensor transforms as
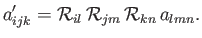 |
(B.34) |
The generalization to higher-order tensors is straightforward. For the case of a scalar, which is a zeroth-order
tensor, the transformation rule is particularly simple: that is,
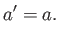 |
(B.35) |
By analogy with Equation (B.27), the inverse transform is
exemplified by
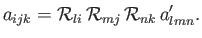 |
(B.36) |
Incidentally, because all tensors of the same order transform in the same manner, it immediately
follows that two tensors of the same order whose components are equal in one particular Cartesian coordinate system
will have their components equal in all coordinate systems that can be obtained from the original
system via rotation of the coordinate axes. In other words,
if
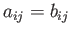 |
(B.37) |
in one particular Cartesian coordinate system then
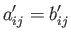 |
(B.38) |
in all Cartesian coordinate systems (with the same origin and system of units as the original system).
Conversely, it does not make sense to equate tensors of different order, because such an equation would
only be valid in one particular coordinate system, and so could not have any physical significance (because the
laws of physics are coordinate independent).
It can easily be shown that the outer product of two tensors transforms as a tensor of the appropriate order.
Thus, if
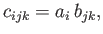 |
(B.39) |
and
then
which is the correct transformation rule for a third-order tensor.
The tensor transformation rule can be combined with the identity (B.29) to show that the
scalar product of two vectors transforms as a scalar. Thus,
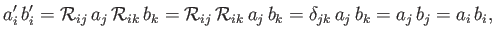 |
(B.43) |
where use has been made of Equation (B.14). Again, the previous proof is more rigorous than that given
in Section A.6. The proof also indicates that the inner product of
two tensors transforms as a tensor of the appropriate order.
The result that both the inner and outer products of two tensors transform as tensors
of the appropriate order is known as the product rule.
Closely related to this rule is the so-called quotient rule, according to which
if (say)
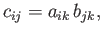 |
(B.44) |
where 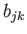 is an arbitrary tensor,
and
is an arbitrary tensor,
and 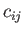 transforms as a tensor under all rotations
of the coordinate axes, then
transforms as a tensor under all rotations
of the coordinate axes, then 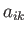 --which can be thought of as the quotient of
--which can be thought of as the quotient of 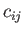 and
and 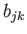 --also transforms as a tensor.
The proof is as follows:
--also transforms as a tensor.
The proof is as follows:
where use has been made of the fact that 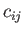 and
and 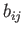 transform as tensors, as well as Equation (B.28).
Rearranging, we obtain
transform as tensors, as well as Equation (B.28).
Rearranging, we obtain
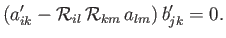 |
(B.46) |
However, the 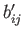 are arbitrary, so the previous equation can only be satisfied, in general, if
are arbitrary, so the previous equation can only be satisfied, in general, if
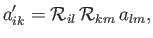 |
(B.47) |
which is the correct transformation rule for a tensor.
Incidentally, the quotient rule applies to any type of valid tensor product.
The components of the second-order identity tensor,
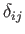 , have the special property that they
are invariant under rotation of the coordinate axes. This follows because
, have the special property that they
are invariant under rotation of the coordinate axes. This follows because
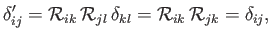 |
(B.48) |
where use has been made of Equation (B.28). The components of the third-order permutation
tensor,
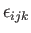 , also have this special property. This follows because
, also have this special property. This follows because
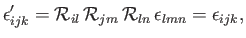 |
(B.49) |
where use has been made of Equation (B.31). The fact that
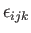 transforms as a proper
third-order tensor immediately implies, from the product rule,
that the vector product of two vectors transforms as a proper vector: that is,
transforms as a proper
third-order tensor immediately implies, from the product rule,
that the vector product of two vectors transforms as a proper vector: that is,
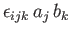 is a first-order tensor provided that
is a first-order tensor provided that 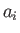 and
and 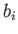 are both first-order tensors.
This proof is much more rigorous that that given earlier in Section A.8.
are both first-order tensors.
This proof is much more rigorous that that given earlier in Section A.8.



Next: Tensor Fields
Up: Cartesian Tensors
Previous: Tensors and Tensor Notation
Richard Fitzpatrick
2016-03-31
![]() , have the special property that they
are invariant under rotation of the coordinate axes. This follows because
, have the special property that they
are invariant under rotation of the coordinate axes. This follows because