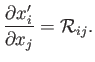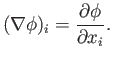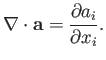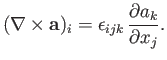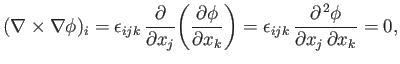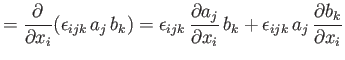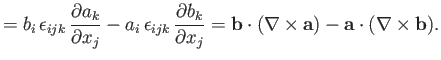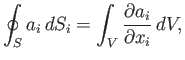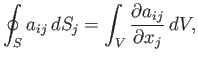Next: Isotropic Tensors
Up: Cartesian Tensors
Previous: Tensor Transformation
Tensor Fields
We saw in Appendix A that a scalar field is a set of scalars associated with every point in space: for instance,
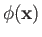 , where
, where
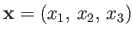 is a position vector. We also saw that a vector field
is a set of vectors associated with every point in space: for instance,
is a position vector. We also saw that a vector field
is a set of vectors associated with every point in space: for instance,
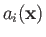 . It stands to reason, then, that
a tensor field is a set of tensors associated with every point in space: for instance,
. It stands to reason, then, that
a tensor field is a set of tensors associated with every point in space: for instance,
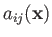 .
It immediately follows that a scalar field is a zeroth-order tensor field, and a vector field is a first-order
tensor field.
.
It immediately follows that a scalar field is a zeroth-order tensor field, and a vector field is a first-order
tensor field.
Most tensor fields encountered in physics are smoothly varying and differentiable. Consider the first-order tensor field
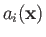 .
The various partial derivatives of the components of this field with respect to the Cartesian coordinates
.
The various partial derivatives of the components of this field with respect to the Cartesian coordinates 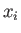 are written
are written
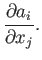 |
(B.50) |
Moreover, this set of derivatives transform as the components of a second-order tensor. In order to demonstrate this, we need the transformation
rule for the 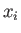 , which is the same as that for a first-order tensor: that is,
, which is the same as that for a first-order tensor: that is,
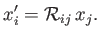 |
(B.51) |
Thus,
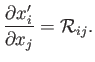 |
(B.52) |
It is also easily shown that
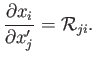 |
(B.53) |
Now,
 |
(B.54) |
which is the correct transformation rule for a second-order tensor. Here, use has been made of the chain rule, as
well as Equation (B.53). [Note, from Equation (B.26), that the
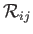 are not
functions of position.]
It follows, from the previous argument, that differentiating a
tensor field increases its order by one: for instance,
are not
functions of position.]
It follows, from the previous argument, that differentiating a
tensor field increases its order by one: for instance,
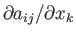 is a third-order tensor. The only
exception to this rule occurs when differentiation and contraction are combined. Thus,
is a third-order tensor. The only
exception to this rule occurs when differentiation and contraction are combined. Thus,
 is a first-order tensor, because it only contains a single free index.
is a first-order tensor, because it only contains a single free index.
The gradient (see Section A.18) of a scalar field is an example of a first-order tensor field (i.e., a vector field):
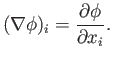 |
(B.55) |
The divergence (see Section A.20) of a vector field is a contracted second-order tensor field that transforms as a scalar:
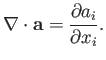 |
(B.56) |
Finally, the curl (see Section A.22) of a vector field is a contracted fifth-order tensor that transforms as a vector
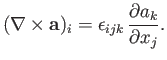 |
(B.57) |
The previous definitions can be used to prove a number of useful results.
For instance,
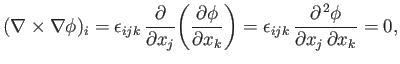 |
(B.58) |
which follows from symmetry because
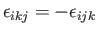 whereas
whereas
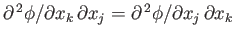 . Likewise,
. Likewise,
 |
(B.59) |
which again follows from symmetry. As a final example,
According to the divergence theorem (see Section A.20),
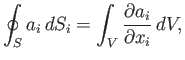 |
(B.61) |
where  is a closed surface surrounding the volume
is a closed surface surrounding the volume  . The previous theorem is
easily generalized to give, for example,
. The previous theorem is
easily generalized to give, for example,
 |
(B.62) |
or
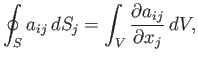 |
(B.63) |
or even
 |
(B.64) |



Next: Isotropic Tensors
Up: Cartesian Tensors
Previous: Tensor Transformation
Richard Fitzpatrick
2016-03-31
![]() .
The various partial derivatives of the components of this field with respect to the Cartesian coordinates
.
The various partial derivatives of the components of this field with respect to the Cartesian coordinates ![]() are written
are written