


Next: Tensor Transformation
Up: Cartesian Tensors
Previous: Introduction
Let the Cartesian coordinates  ,
,  ,
,  be written as the
be written as the 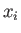 , where
, where 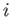 runs from 1 to 3. In other words,
runs from 1 to 3. In other words,
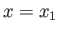 ,
, 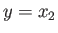 , and
, and 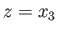 . Incidentally, in the following, any lowercase roman subscript (e.g.,
. Incidentally, in the following, any lowercase roman subscript (e.g., 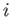 ,
,  ,
, 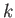 ) is
assumed to run from 1 to 3. We can also write the Cartesian components of a general vector
) is
assumed to run from 1 to 3. We can also write the Cartesian components of a general vector 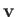 as the
as the  . In other words,
. In other words, 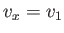 ,
, 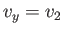 , and
, and 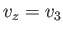 . By contrast, a scalar is represented as
a variable without a subscript: for instance,
. By contrast, a scalar is represented as
a variable without a subscript: for instance,  ,
, 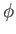 . Thus, a scalar--which is a tensor of order zero--is
represented as a variable with zero subscripts, and a vector--which is a tensor of order one--is
represented as a variable with one subscript. It stands to reason, therefore, that a tensor of order two is
represented as a variable with two subscripts: for instance,
. Thus, a scalar--which is a tensor of order zero--is
represented as a variable with zero subscripts, and a vector--which is a tensor of order one--is
represented as a variable with one subscript. It stands to reason, therefore, that a tensor of order two is
represented as a variable with two subscripts: for instance, 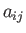 ,
,
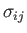 . Moreover, an
. Moreover, an 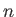 th-order tensor is represented as a variable with
th-order tensor is represented as a variable with 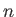 subscripts: for instance,
subscripts: for instance, 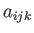 is a third-order tensor, and
is a third-order tensor, and  a fourth-order tensor.
Note that a general
a fourth-order tensor.
Note that a general 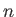 th-order tensor has
th-order tensor has  independent components.
independent components.
The
components of a second-order tensor are conveniently visualized as a two-dimensional matrix, just as
the components of a vector are sometimes visualized as a one-dimensional matrix. However, it
is important to recognize that an 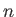 th-order tensor is not simply another name for an
th-order tensor is not simply another name for an 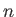 -dimensional matrix. A matrix is
merely an ordered set of numbers. A tensor, on the other hand, is an ordered set of components
that have specific transformation properties under rotation of the coordinate axes. (See Section B.3.)
-dimensional matrix. A matrix is
merely an ordered set of numbers. A tensor, on the other hand, is an ordered set of components
that have specific transformation properties under rotation of the coordinate axes. (See Section B.3.)
Consider two vectors  and
and  that are represented as
that are represented as 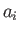 and
and 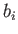 , respectively, in
tensor notation. According to Section A.6, the scalar product of these two vectors
takes the form
, respectively, in
tensor notation. According to Section A.6, the scalar product of these two vectors
takes the form
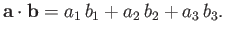 |
(B.1) |
The previous expression can be written more compactly as
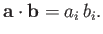 |
(B.2) |
Here, we have made use of the Einstein summation convention, according to which, in an expression
containing lower case roman subscripts, any subscript that appears twice (and only twice) in any
term of the expression is assumed to be summed from 1 to 3 (unless stated otherwise).
Thus,
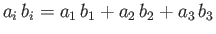 , and
, and
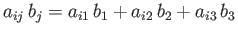 .
Note that when an index is summed it becomes a dummy index and can be written as any
(unique) symbol: that is,
.
Note that when an index is summed it becomes a dummy index and can be written as any
(unique) symbol: that is,
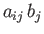 and
and
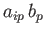 are equivalent.
Moreover, only non-summed, or free, indices count toward the order of a tensor expression. Thus,
are equivalent.
Moreover, only non-summed, or free, indices count toward the order of a tensor expression. Thus,
 is a zeroth-order tensor (because there are no free indices), and
is a zeroth-order tensor (because there are no free indices), and
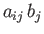 is a first-order tensor (because there
is only one free index). The process of reducing the order of a tensor expression by summing indices is known
as contraction. For example,
is a first-order tensor (because there
is only one free index). The process of reducing the order of a tensor expression by summing indices is known
as contraction. For example,  is a zeroth-order contraction of the second-order tensor
is a zeroth-order contraction of the second-order tensor 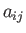 .
Incidentally, when two tensors are multiplied together without contraction the
resulting tensor is called an outer product: for instance, the second-order tensor
.
Incidentally, when two tensors are multiplied together without contraction the
resulting tensor is called an outer product: for instance, the second-order tensor 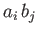 is the
outer product of the two first-order tensors
is the
outer product of the two first-order tensors 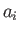 and
and 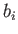 . Likewise, when two tensors are multiplied
together in a manner that involves contraction then the resulting tensor is called an inner product:
for instance, the first-order tensor
. Likewise, when two tensors are multiplied
together in a manner that involves contraction then the resulting tensor is called an inner product:
for instance, the first-order tensor
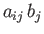 is an inner product of the second-order tensor
is an inner product of the second-order tensor 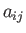 and
the first-order tensor
and
the first-order tensor 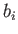 . It can be seen from Equation (B.2) that the scalar product of two
vectors is equivalent to the inner product of the corresponding first-order tensors.
. It can be seen from Equation (B.2) that the scalar product of two
vectors is equivalent to the inner product of the corresponding first-order tensors.
According to Section A.8, the vector product of two vectors  and
and  takes the form
takes the form
in tensor notation.
The previous expression can be written more compactly as
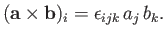 |
(B.6) |
Here,
![$\displaystyle \epsilon_{ijk} = \left\{ \begin{array}{lll} +1&\mbox{\hspace{0.5c...
... odd permutation of $1, 2, 3$}\\ [0.5ex] 0&&\mbox{otherwise} \end{array}\right.$](img6787.png) |
(B.7) |
is known as the third-order permutation tensor (or, sometimes, the third-order Levi-Civita tensor). Note, in particular, that
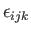 is zero if one of its indices is
repeated: for instance,
is zero if one of its indices is
repeated: for instance,
 .
Furthermore, it follows from Equation (B.7) that
.
Furthermore, it follows from Equation (B.7) that
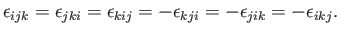 |
(B.8) |
It is helpful to define the second-order identity tensor (also known as the Kroenecker delta tensor),
![$\displaystyle \delta_{ij} = \left\{ \begin{array}{lll} 1&\mbox{\hspace{0.5cm}}& \mbox{if $i=j$}\\ [0.5ex] 0&&\mbox{otherwise} \end{array}\right. .$](img6790.png) |
(B.9) |
It is easily seen that
et cetera.
The following is a particularly important tensor identity:
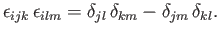 |
(B.16) |
In order to establish the validity of the previous expression, let us consider the various cases that arise.
As is easily seen, the right-hand side of Equation (B.16) takes the values
Moreover, in each product on the left-hand side of Equation (B.16), 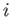 has the same value in both
has the same value in both  factors. Thus,
for a non-zero contribution,
none of
factors. Thus,
for a non-zero contribution,
none of  ,
, 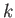 ,
, 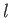 , and
, and 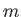 can have the same value as
can have the same value as 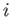 (because each
(because each  factor is zero if any of its
indices are repeated). Because a given subscript
can only take one of three values (
factor is zero if any of its
indices are repeated). Because a given subscript
can only take one of three values (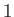 ,
, 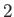 , or
, or  ), the only possibilities that
generate non-zero contributions are
), the only possibilities that
generate non-zero contributions are 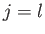 and
and  , or
, or 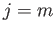 and
and 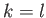 , excluding
, excluding 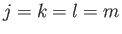 (as
each
(as
each  factor would then have repeated indices, and so be zero). Thus, the left-hand side of Equation (B.16) reproduces Equation (B.19), as well as the conditions on the indices in
Equations (B.17) and (B.18). The left-hand side also reproduces the values in Equations (B.17) and (B.18) because if
factor would then have repeated indices, and so be zero). Thus, the left-hand side of Equation (B.16) reproduces Equation (B.19), as well as the conditions on the indices in
Equations (B.17) and (B.18). The left-hand side also reproduces the values in Equations (B.17) and (B.18) because if 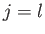 and
and  then
then
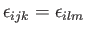 and the product
and the product
 (no summation) is equal to
(no summation) is equal to 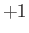 , whereas
if
, whereas
if 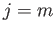 and
and 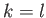 then
then
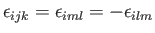 and the
product
and the
product
 (no summation) is equal to
(no summation) is equal to 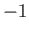 . Here, use has been made of Equation (B.8).
Hence, the validity of the identity (B.16) has been established.
. Here, use has been made of Equation (B.8).
Hence, the validity of the identity (B.16) has been established.
In order to illustrate the use of Equation (B.16), consider the vector triple product
identity (see Section A.11)
 |
(B.20) |
In tensor notation, the left-hand side of this identity is written
![$\displaystyle [{\bf a}\times ({\bf b}\times {\bf c})]_i = \epsilon_{ijk}\,a_j\,(\epsilon_{klm}\,b_l\,c_m),$](img6817.png) |
(B.21) |
where use has been made of Equation (B.6). Employing Equations (B.8) and (B.16), this
becomes
![$\displaystyle [{\bf a}\times ({\bf b}\times {\bf c})]_i = \epsilon_{kij}\,\epsi...
... = \left(\delta_{il}\,\delta_{jm}-\delta_{im}\,\delta_{jl}\right)a_j\,b_l\,c_m,$](img6818.png) |
(B.22) |
which, with the aid of Equations (B.2) and (B.13), reduces to
![$\displaystyle [{\bf a}\times ({\bf b}\times {\bf c})]_i = a_j\,c_j\,b_i - a_j\,...
...\left[({\bf a}\cdot{\bf c})\,{\bf b} - ({\bf a}\cdot{\bf b})\,{\bf c}\right]_i.$](img6819.png) |
(B.23) |
Thus, we have established the validity of the vector identity (B.20).
Moreover, our proof is much more rigorous than that given earlier in Section A.11.



Next: Tensor Transformation
Up: Cartesian Tensors
Previous: Introduction
Richard Fitzpatrick
2016-03-31
![]() th-order tensor is not simply another name for an
th-order tensor is not simply another name for an ![]() -dimensional matrix. A matrix is
merely an ordered set of numbers. A tensor, on the other hand, is an ordered set of components
that have specific transformation properties under rotation of the coordinate axes. (See Section B.3.)
-dimensional matrix. A matrix is
merely an ordered set of numbers. A tensor, on the other hand, is an ordered set of components
that have specific transformation properties under rotation of the coordinate axes. (See Section B.3.)
![]() and
and ![]() that are represented as
that are represented as ![]() and
and ![]() , respectively, in
tensor notation. According to Section A.6, the scalar product of these two vectors
takes the form
, respectively, in
tensor notation. According to Section A.6, the scalar product of these two vectors
takes the form
![]() and
and ![]() takes the form
takes the form