


Next: Response to Equilibrium Harmonic
Up: Terrestrial Ocean Tides
Previous: Laplace Tidal Equations
Making use of Equations (12.25)-(12.27), (12.35), (12.44), (12.65), and (12.80), we can write the
forcing term in the Laplace tidal equations in the form
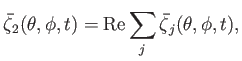 |
(12.138) |
where
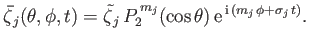 |
(12.139) |
The amplitudes,
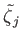 , azimuthal mode numbers,
, azimuthal mode numbers, 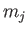 , and frequencies,
, and frequencies, 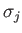 , of the principal
harmonics of the forcing term are specified in Table 12.1, where
, of the principal
harmonics of the forcing term are specified in Table 12.1, where
Here, 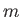 is the planetary mass,
is the planetary mass, 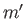 the mass of the moon, and
the mass of the moon, and 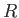 the moon's orbital major radius.
As indicated in the table, the harmonics of the forcing term can be divided into four classes: an ``equilibrium'' term that is time independent;
two ``long period'' terms that oscillate with periods much longer than the planet's diurnal (i.e., rotational) period; two ``diurnal'' terms that
oscillate at periods close to the planet's diurnal period; and two ``semi-diurnal'' terms that oscillate at periods
close to half the planet's diurnal period. Here, we have neglected a semi-diurnal term that is significantly smaller than the other two.
the moon's orbital major radius.
As indicated in the table, the harmonics of the forcing term can be divided into four classes: an ``equilibrium'' term that is time independent;
two ``long period'' terms that oscillate with periods much longer than the planet's diurnal (i.e., rotational) period; two ``diurnal'' terms that
oscillate at periods close to the planet's diurnal period; and two ``semi-diurnal'' terms that oscillate at periods
close to half the planet's diurnal period. Here, we have neglected a semi-diurnal term that is significantly smaller than the other two.
Table 12.2:
The principal harmonics of the forcing term in the Laplace tidal equations for the Earth.
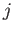
|
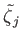
|
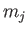
|
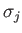
|
Classification |
Symbol |
| |
|
|
|
|
|
| |
|
|
|
|
|
| 0
|
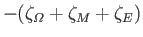
|
0 |
0
|
Equilibrium |
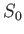 ,
, 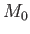
|
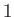
|
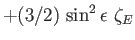
|
0 |
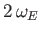
|
Long Period |
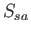
|
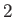
|
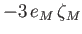
|
0 |
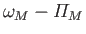
|
Long Period |
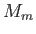
|
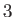
|
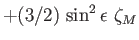
|
0 |
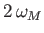
|
Long Period |
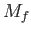
|
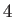
|
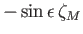
|
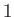
|
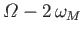
|
Diurnal |
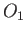
|
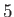
|
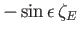
|
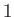
|
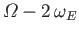
|
Diurnal |
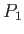
|
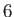
|
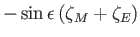
|
1 |
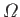
|
Diurnal |
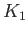
|
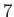
|
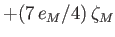
|
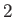
|
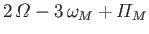
|
Semi-diurnal |
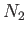
|
|
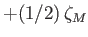
|
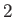
|
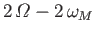
|
Semi-diurnal |
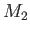
|
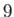
|
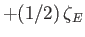
|
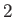
|
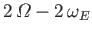
|
Semi-diurnal |
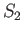
|
|
For the Earth-Moon system,
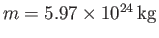 ,
,
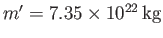 ,
,
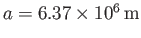 ,
,
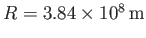 ,
,
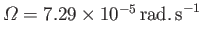 (Yoder 1995). It follows that
(Yoder 1995). It follows that
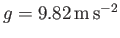 , as
well as
, as
well as
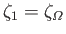 ,
,
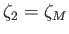 , where
, where
Moreover,
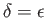 ,
, 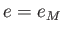 ,
,
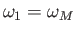 , and
, and
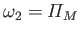 , where
, where
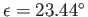 ,
,
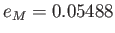 ,
,
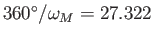 (solar) days,
(solar) days,
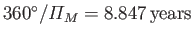 (Yoder 1995). Here,
(Yoder 1995). Here, 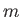 ,
, 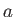 ,
,
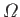 , and
, and 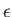 are the Earth's mass, mean radius, (sidereal) rotational angular velocity, and inclination of the equatorial plane to the ecliptic, respectively.
Furthermore,
are the Earth's mass, mean radius, (sidereal) rotational angular velocity, and inclination of the equatorial plane to the ecliptic, respectively.
Furthermore, 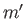 ,
, 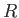 ,
, 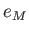 ,
, 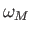 , and
, and
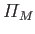 are the Moon's mass, orbital major radius, orbital eccentricity, mean orbital
angular velocity, and rate of perigee precession, respectively. Here, we have neglected the small (i.e., about
are the Moon's mass, orbital major radius, orbital eccentricity, mean orbital
angular velocity, and rate of perigee precession, respectively. Here, we have neglected the small (i.e., about 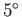 ) inclination of the Moon's orbital plane
to the ecliptic.
) inclination of the Moon's orbital plane
to the ecliptic.
For the Earth-Sun system,
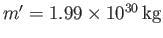 and
and
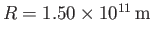 (Yoder 1995). It follows that
(Yoder 1995). It follows that
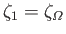 and
and
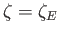 , where
, where
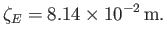 |
(12.144) |
Moreover,
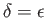 ,
, 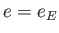 ,
,
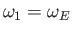 , and
, and
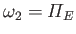 , where
, where
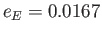 ,
,
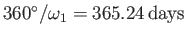 , and
, and
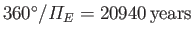 (Yoder 1995). Here,
(Yoder 1995). Here, 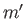 is the solar mass. Furthermore,
is the solar mass. Furthermore, 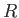 ,
, 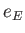 ,
, 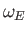 ,
and
,
and
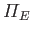 are the Earth's orbital major radius, orbital eccentricity, mean orbital angular velocity, and rate of perihelion precession, respectively.
are the Earth's orbital major radius, orbital eccentricity, mean orbital angular velocity, and rate of perihelion precession, respectively.
Combining lunar and solar effects, we can write the
forcing term in the Laplace tidal equations for the Earth in the form (12.142)-(12.143).
The properties of the principal
harmonics of the forcing term are specified in Tables 12.2 and 12.3. The symbols are due to G.H. Darwin (1845-1912).
Table 12.3:
The principal harmonics of the forcing term in the Laplace tidal equations for the Earth, excluding the equilibrium harmonic.
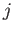
|
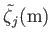
|
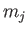
|
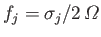
|
Period |
Symbol |
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
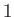
|
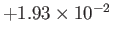
|
0 |
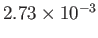
|
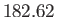 days
days |
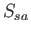
|
|
|
|
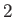
|
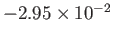
|
0 |
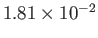
|
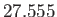 days
days |
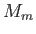
|
|
|
|
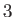
|
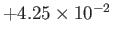
|
0 |
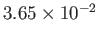
|
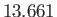 days
days |
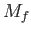
|
|
|
|
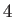
|
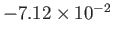
|
1 |
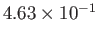
|
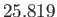 hours
hours |
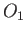
|
|
|
|
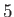
|
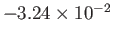
|
1 |
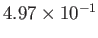
|
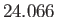 hours
hours |
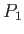
|
|
|
|
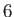
|
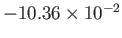
|
1 |
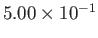
|
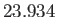 hours
hours |
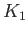
|
|
|
|
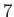
|
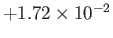
|
2 |
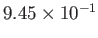
|
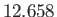 hours
hours |
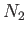
|
|
|
|
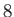
|
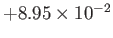
|
2 |
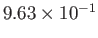
|
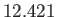 hours
hours |
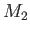
|
|
|
|
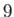
|
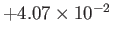
|
2 |
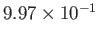
|
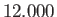 hours
hours |
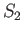
|
|
|
|
|



Next: Response to Equilibrium Harmonic
Up: Terrestrial Ocean Tides
Previous: Laplace Tidal Equations
Richard Fitzpatrick
2016-03-31
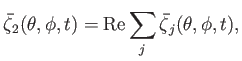
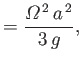
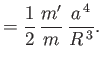
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (Yoder 1995). It follows that
(Yoder 1995). It follows that
![]() , as
well as
, as
well as
![]() ,
,
![]() , where
, where
![]() and
and
![]() (Yoder 1995). It follows that
(Yoder 1995). It follows that
![]() and
and
![]() , where
, where