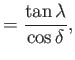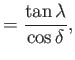Next: Surface Harmonics and Solid
Up: Terrestrial Ocean Tides
Previous: Decomposition of Tide Generating
Suppose that, in the  ,
,  ,
, 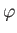 frame, the moon's orbit is a Keplerian ellipse of major radius
frame, the moon's orbit is a Keplerian ellipse of major radius 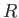 , and eccentricity
, and eccentricity 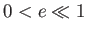 , lying in a fixed plane that is
inclined at an angle
, lying in a fixed plane that is
inclined at an angle 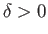 to the plane
to the plane
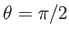 . Thus, the closest and furthest distance between the centers of the moon and the planet are
. Thus, the closest and furthest distance between the centers of the moon and the planet are
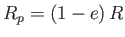 and
and
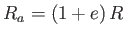 , respectively.
It follows that (Fitzpatrick 2013)
, respectively.
It follows that (Fitzpatrick 2013)
where
Here, it is assumed that the closest point on the moon's orbit to the center of the planet corresponds to
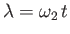 , where
, where 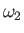 is the uniform precession rate of this point. [It is necessary to include such precession in our analysis because the Moon's perigee precesses steadily in such a manner that it completes an orbit about the Earth once every 8.85 years. This effect is caused by the perturbing influence of the Sun (Fitzpatrick 2013).]
Suppose that the inclination of the moon's orbit to the planet's equatorial plane,
is the uniform precession rate of this point. [It is necessary to include such precession in our analysis because the Moon's perigee precesses steadily in such a manner that it completes an orbit about the Earth once every 8.85 years. This effect is caused by the perturbing influence of the Sun (Fitzpatrick 2013).]
Suppose that the inclination of the moon's orbit to the planet's equatorial plane,
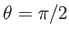 , is relatively small, so that
, is relatively small, so that
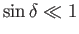 .
It follows that
.
It follows that
Thus, Equations (12.22)-(12.24), (12.28), and (12.32)-(12.34) can be combined to give the following expression for the tide generating potential due to a moon in a low-eccentricity, low-inclination
orbit:
Here, we have retained a term proportional to
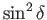 in the previous expression, despite the
fact that we are formally neglecting
in the previous expression, despite the
fact that we are formally neglecting
 terms, because the term in question gives rise to
important fortnightly tides on the Earth.
terms, because the term in question gives rise to
important fortnightly tides on the Earth.



Next: Surface Harmonics and Solid
Up: Terrestrial Ocean Tides
Previous: Decomposition of Tide Generating
Richard Fitzpatrick
2016-03-31