Next: Terrestrial Ocean Tides
Up: Waves in Incompressible Fluids
Previous: Wind Driven Waves in
- Find the velocity potential of a standing gravity wave in deep water for which the
associated elevation of the free surface is
Determine the paths of water particles perturbed by the wave.
- Deep water fills a rectangular tank of length
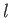 and breadth
and breadth 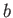 . Show that the resonant frequencies of the
water in the tank are
. Show that the resonant frequencies of the
water in the tank are
where 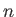 and
and 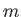 are integers. Neglect surface tension.
are integers. Neglect surface tension.
- Demonstrate that a sinusoidal gravity wave on deep water with surface elevation
possesses a mean momentum per unit surface area
- A seismic wave passes along the bed of an ocean of uniform depth
 such that the vertical
perturbation of the bed is
such that the vertical
perturbation of the bed is
![$ a\,\cos[k\,(x-V\,t)]$](img4206.png) . Show that the amplitude of the consequent gravity waves
at the surface is
. Show that the amplitude of the consequent gravity waves
at the surface is
where 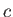 is the phase velocity of waves of wavenumber
is the phase velocity of waves of wavenumber 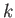 .
.
- A layer of liquid of density
 and depth
and depth  has a free upper surface, and lies over
liquid of infinite depth and density
has a free upper surface, and lies over
liquid of infinite depth and density
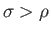 . Neglecting surface tension, show
that two possible types of wave of wavenumber
. Neglecting surface tension, show
that two possible types of wave of wavenumber 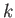 , with
phase velocities
, with
phase velocities
can propagate along the layer.
- Show that, taking surface tension into account, a sinusoidal wave of wavenumber
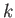 and surface amplitude
and surface amplitude  has a mean
kinetic energy per unit surface area
has a mean
kinetic energy per unit surface area
and a mean potential energy per unit surface area
- Show that in water of uniform depth
 the phase velocity of surface waves can only attain a stationary (i.e., maximum or minimum) value
as a function of wavenumber,
the phase velocity of surface waves can only attain a stationary (i.e., maximum or minimum) value
as a function of wavenumber, 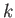 , when
, when
where
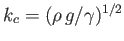 . Hence, deduce that the phase velocity has just one stationary value (a minimum) for any
depth greater than
. Hence, deduce that the phase velocity has just one stationary value (a minimum) for any
depth greater than
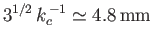 , but no stationary values for depths less than that.
, but no stationary values for depths less than that.
- Unlike gravity waves in deep water, whose group velocities are half their phase velocities, the group velocities of capillary waves are
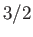 times their phase velocities. Adapt the analysis of
Section 11.7 to investigate the generation of capillary waves by a very small object traveling across the surface of the water at
the constant speed
times their phase velocities. Adapt the analysis of
Section 11.7 to investigate the generation of capillary waves by a very small object traveling across the surface of the water at
the constant speed  . Suppose that the unperturbed surface corresponds to the
. Suppose that the unperturbed surface corresponds to the  -
- plane.
Let the object travel in the minus
plane.
Let the object travel in the minus  -direction, such that it is instantaneously found at the origin. Find the present
position of waves that were emitted, traveling at an angle
-direction, such that it is instantaneously found at the origin. Find the present
position of waves that were emitted, traveling at an angle  to the object's direction of motion, when it was located at
to the object's direction of motion, when it was located at 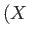 ,
,  .
Show that along a given interference maximum the quantities
.
Show that along a given interference maximum the quantities 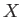 and
and  vary in such a manner that
vary in such a manner that
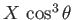 takes a constant value,
takes a constant value, 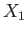 (say). Deduce that the interference maximum is given parametrically by the equations
(say). Deduce that the interference maximum is given parametrically by the equations
Sketch this curve, noting that it goes through the points
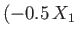 ,
,  and
and 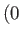 ,
,
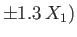 , and asymptotes to
, and asymptotes to
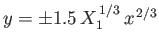 .
.



Next: Terrestrial Ocean Tides
Up: Waves in Incompressible Fluids
Previous: Wind Driven Waves in
Richard Fitzpatrick
2016-03-31
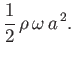
![$\displaystyle a\left[\left(1-\frac{c^{\,2}}{V^{\,2}}\right)\cosh (k\,d)\right]^{\,-1},
$](img4207.png)
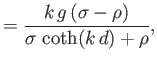
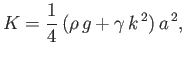
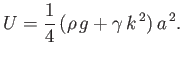
![$\displaystyle k = \left[\frac{\sinh(2\,k\,d)-2\,k\,d}{\sinh(2\,k\,d)+2\,k\,d}\right]^{1/2} k_c,
$](img4214.png)