


Next: Exercises
Up: Waves in Incompressible Fluids
Previous: Capillary Waves at an
Consider the scenario described in the previous section.
Suppose that the lower fluid is a body of deep water at rest, and the upper fluid is the atmosphere. Let the air above
the surface of the water move horizontally at the constant velocity 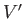 .
Suppose that
.
Suppose that  is the density of water,
is the density of water,
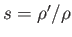 the specific gravity of air with respect to water, and
the specific gravity of air with respect to water, and 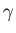 the
surface tension at an air/water interface. With
the
surface tension at an air/water interface. With  ,
,
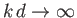 ,
,
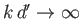 , the dispersion relation (11.132)
reduces to
, the dispersion relation (11.132)
reduces to
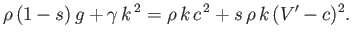 |
(11.139) |
This expression can be rearranged to give
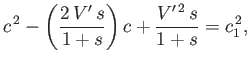 |
(11.140) |
which is a quadratic equation for the phase velocity, 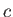 , of the wave. Here,
, of the wave. Here,
 |
(11.141) |
where  is the phase velocity that the wave would
have in the absence of the wind. In fact, we can write
is the phase velocity that the wave would
have in the absence of the wind. In fact, we can write
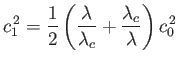 |
(11.142) |
where
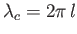 is the capillary wavelength, and
is the capillary wavelength, and 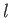 and
and 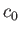 are defined in Equations (11.134) and (11.135), respectively.
are defined in Equations (11.134) and (11.135), respectively.
For a given wavelength, 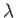 , the wave velocity,
, the wave velocity, 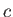 , attains its maximum value,
, attains its maximum value, 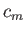 , when
, when 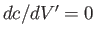 . According to the dispersion
relation (11.140), this occurs when
. According to the dispersion
relation (11.140), this occurs when
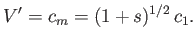 |
(11.143) |
If the wind has any other velocity, greater or less than 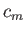 , then the wave velocity is less than
, then the wave velocity is less than 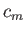 .
.
According to Equation (11.140), the wave velocity, 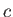 , becomes complex, indicating an instability, when
, becomes complex, indicating an instability, when
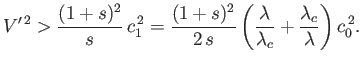 |
(11.144) |
We conclude that if the wind speed exceeds the critical value
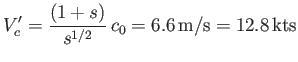 |
(11.145) |
then waves whose wavelengths fall within a certain range, centered around 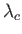 , are unstable and grow to large amplitude.
, are unstable and grow to large amplitude.
The two roots of Equation (11.140) are
![$\displaystyle c = \frac{V'\,s}{1+s} \pm\left[c_1^{\,2}- \frac{s\,V'^{\,2}}{(1+s)^2}\right]^{1/2}.$](img4199.png) |
(11.146) |
Moreover, if
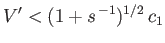 |
(11.147) |
then these roots have opposite signs. Hence, the waves can either travel with the wind, or against it, but travel faster when they
are moving with the wind. If 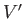 exceeds the value given previously then the waves cannot travel against the wind. Because
exceeds the value given previously then the waves cannot travel against the wind. Because  has the minimum value
has the minimum value 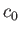 , it follows that waves traveling against the wind are completely ruled out when
, it follows that waves traveling against the wind are completely ruled out when
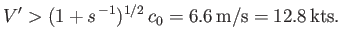 |
(11.148) |



Next: Exercises
Up: Waves in Incompressible Fluids
Previous: Capillary Waves at an
Richard Fitzpatrick
2016-03-31

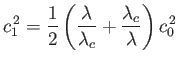
![]() , the wave velocity,
, the wave velocity, ![]() , attains its maximum value,
, attains its maximum value, ![]() , when
, when ![]() . According to the dispersion
relation (11.140), this occurs when
. According to the dispersion
relation (11.140), this occurs when
![]() , becomes complex, indicating an instability, when
, becomes complex, indicating an instability, when
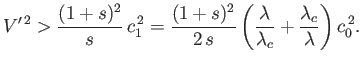
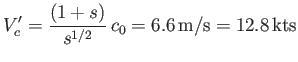
![$\displaystyle c = \frac{V'\,s}{1+s} \pm\left[c_1^{\,2}- \frac{s\,V'^{\,2}}{(1+s)^2}\right]^{1/2}.$](img4199.png)