


Next: Axisymmetric Stokes Flow
Up: Incompressible Viscous Flow
Previous: Lubrication Theory
Steady flow in which the viscous force density in the fluid greatly exceeds the advective inertia per unit volume is generally known
as Stokes flow, in honor of George Stokes (1819-1903). Because, by definition, the Reynolds number of a fluid is the typical ratio of the advective inertia per unit volume to the viscous force density (see Section 1.16), Stokes flow implies Reynolds numbers that are much less than unity.
In the time independent, low Reynolds number limit, Equations (10.1) and (10.2) reduce to
It follows from these equations that
where

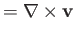 , and use has been made of Equation (A.177). Taking the curl of this
expression, we obtain
, and use has been made of Equation (A.177). Taking the curl of this
expression, we obtain
which is the governing equation for Stokes flow.
Here, use has been made of Equations (A.173), (A.176), and (A.177).



Next: Axisymmetric Stokes Flow
Up: Incompressible Viscous Flow
Previous: Lubrication Theory
Richard Fitzpatrick
2016-03-31