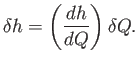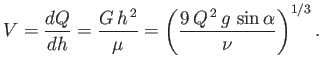Next: Poiseuille Flow
Up: Incompressible Viscous Flow
Previous: Flow Between Parallel Plates
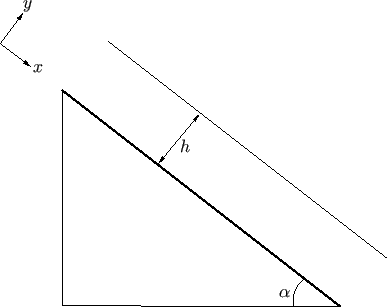
Consider steady, two-dimensional, viscous flow down a plane that is inclined at an angle  to the
horizontal. Let
to the
horizontal. Let  measure distance along the plane, and let
measure distance along the plane, and let  be a transverse coordinate such that the surface of the plane corresponds
to
be a transverse coordinate such that the surface of the plane corresponds
to  . Suppose that the fluid forms a uniform layer of depth
. Suppose that the fluid forms a uniform layer of depth 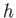 covering this surface. (See Figure 10.2.)
covering this surface. (See Figure 10.2.)
Figure 10.2:
Viscous flow down an inclined plane.
 |
The generalized pressure gradient within the fluid is written
 |
(10.12) |
where 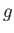 is the acceleration due to gravity. In this case, there is no gradient in the actual pressure in the
is the acceleration due to gravity. In this case, there is no gradient in the actual pressure in the  -direction, and
the flow down the plane is driven entirely by gravity. As before, we can write
-direction, and
the flow down the plane is driven entirely by gravity. As before, we can write
 |
(10.13) |
and Equation (10.2) again reduces to
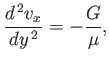 |
(10.14) |
where
 |
(10.15) |
Application of the no slip condition at the surface of the plane,  , yields the standard boundary condition
, yields the standard boundary condition 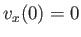 . However, the appropriate physical constraint at the fluid/air interface,
. However, the appropriate physical constraint at the fluid/air interface, 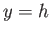 , is that the
normal viscous stress there be zero (i.e.,
, is that the
normal viscous stress there be zero (i.e.,
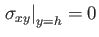 ), because there is nothing above the interface that can exchange momentum with the fluid (assuming that
the finite inertia and viscosity of air are both negligible.) Hence, from Section 1.18, we get the boundary condition
), because there is nothing above the interface that can exchange momentum with the fluid (assuming that
the finite inertia and viscosity of air are both negligible.) Hence, from Section 1.18, we get the boundary condition
 |
(10.16) |
The solution to Equation (10.14) that satisfies the boundary conditions is
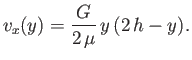 |
(10.17) |
Thus, the profile is again parabolic. In fact, it is the same as the lower half of the profile obtained when fluid flows between two (stationary) parallel plates situated a
perpendicular distance 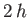 apart.
apart.
The net volume flux (per unit width in the  -direction) of fluid down the plane is
-direction) of fluid down the plane is
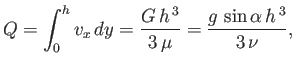 |
(10.18) |
where use has been made of Equation (10.15). Here,
 is the kinematic viscosity of the fluid.
Thus, given the rate
is the kinematic viscosity of the fluid.
Thus, given the rate  that fluid is poured down the plane, the depth of the layer covering the
plane becomes
that fluid is poured down the plane, the depth of the layer covering the
plane becomes
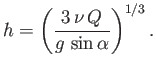 |
(10.19) |
Suppose that the rate at which fluid is poured down the plane is suddenly increased slightly from  to
to
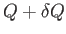 .
We would expect an associated change in depth of the layer covering the plane from
.
We would expect an associated change in depth of the layer covering the plane from 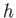 to
to
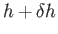 , where
, where
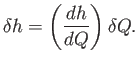 |
(10.20) |
Let the interface between the layers of different depth propagate in the  -direction at the constant velocity
-direction at the constant velocity  . In a frame
of reference that co-moves with this interface, the volume fluxes (per unit width) immediately to the right and to the left
of the interface are
. In a frame
of reference that co-moves with this interface, the volume fluxes (per unit width) immediately to the right and to the left
of the interface are 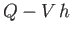 and
and
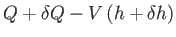 , respectively. However, in a steady state, these fluxes must equal
one another. Hence,
, respectively. However, in a steady state, these fluxes must equal
one another. Hence,
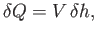 |
(10.21) |
or
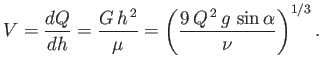 |
(10.22) |
As can easily be verified, this velocity is twice the maximum fluid velocity in the layer.



Next: Poiseuille Flow
Up: Incompressible Viscous Flow
Previous: Flow Between Parallel Plates
Richard Fitzpatrick
2016-03-31



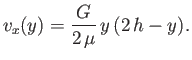
![]() -direction) of fluid down the plane is
-direction) of fluid down the plane is
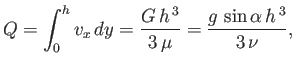
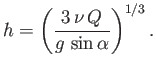
![]() to
to
![]() .
We would expect an associated change in depth of the layer covering the plane from
.
We would expect an associated change in depth of the layer covering the plane from ![]() to
to
![]() , where
, where