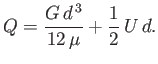Next: Flow Down an Inclined
Up: Incompressible Viscous Flow
Previous: Introduction
Flow Between Parallel Plates
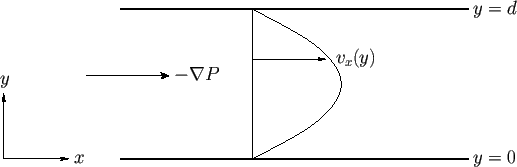
Consider steady, two-dimensional, viscous flow between two parallel plates that are situated a perpendicular distance  apart. Let
apart. Let  be a longitudinal coordinate measuring distance along
the plates, and let
be a longitudinal coordinate measuring distance along
the plates, and let  be a transverse coordinate such that the plates are located at
be a transverse coordinate such that the plates are located at  and
and 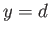 . (See Figure 10.1.)
. (See Figure 10.1.)
Figure 10.1:
Viscous flow between parallel plates.
 |
Suppose that there is a uniform effective pressure gradient in the  -direction, so that
-direction, so that
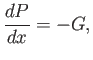 |
(10.4) |
where 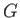 is a constant.
Here, the quantity
is a constant.
Here, the quantity 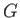 could represent a gradient in actual fluid pressure, a gradient in gravitational potential energy (due to an inclination of the plates to
the horizontal), or
some combination of the two--it actually makes no difference to the final result. Suppose that the fluid velocity profile between the plates takes the form
could represent a gradient in actual fluid pressure, a gradient in gravitational potential energy (due to an inclination of the plates to
the horizontal), or
some combination of the two--it actually makes no difference to the final result. Suppose that the fluid velocity profile between the plates takes the form
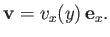 |
(10.5) |
From Section 1.18, this profile automatically satisfies the incompressibility constraint
 , and is also such that
, and is also such that
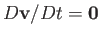 .
Hence, Equation (10.2) reduces to
.
Hence, Equation (10.2) reduces to
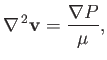 |
(10.6) |
or. taking the  -component,
-component,
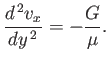 |
(10.7) |
If the two plates are stationary then the solution that satisfies the no slip constraint (see Section 8.2),
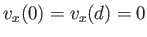 , at each plate is
, at each plate is
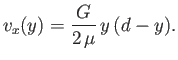 |
(10.8) |
Thus, steady, two-dimensional, viscous flow between two stationary parallel plates is associated with a parabolic velocity profile
that is symmetric about the midplane, 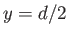 .
The net volume flux (per unit width in the
.
The net volume flux (per unit width in the  -direction) of fluid between the plates is
-direction) of fluid between the plates is
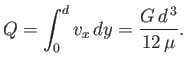 |
(10.9) |
Note that this flux is directly proportional to the effective pressure gradient, inversely proportional to the fluid viscosity, and
increases as the cube of the distance between the plates.
Suppose that the upper plate is stationary, but that the lower plate is moving in the  -direction at the constant speed
-direction at the constant speed 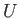 . In this
case, the no slip boundary condition at the lower plate becomes
. In this
case, the no slip boundary condition at the lower plate becomes 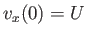 , and the modified solution to Equation (10.7) is
, and the modified solution to Equation (10.7) is
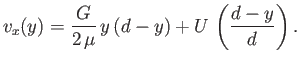 |
(10.10) |
Hence, the modified velocity profile is a combination of parabolic
and linear profiles. This type of flow is known as Couette flow, in honor of Maurice Couette (1858-1943). The net volume flux (per unit width) of fluid between the plates becomes
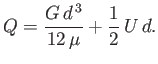 |
(10.11) |



Next: Flow Down an Inclined
Up: Incompressible Viscous Flow
Previous: Introduction
Richard Fitzpatrick
2016-03-31

![]() -direction, so that
-direction, so that
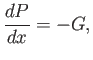
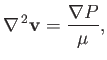
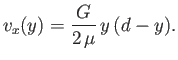
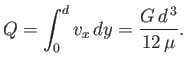
![]() -direction at the constant speed
-direction at the constant speed ![]() . In this
case, the no slip boundary condition at the lower plate becomes
. In this
case, the no slip boundary condition at the lower plate becomes ![]() , and the modified solution to Equation (10.7) is
, and the modified solution to Equation (10.7) is