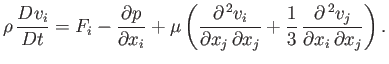Navier-Stokes Equation

Equations (1.24), (1.26), and (1.53) can be combined to give the equation of motion of an isotropic, Newtonian, classical fluid:

$$\rho \,\frac{D v_i}{Dt}= F_i - \frac{\partial p}{\partial x_i} + ... ...partial x_i}\!\left(\frac{2}{3}\,\mu\,\frac{\partial v_j}{\partial x_j}\right).$$ (1.54)

This equation is generally known as the Navier-Stokes equation, and is named after Claude-Louis Navier (1785-1836) and George Gabriel Stokes (1819-1903). In situations in which there are no strong temperature gradients in the fluid, it is a good approximation to treat viscosity as a spatially uniform quantity, in which case the Navier-Stokes equation simplifies somewhat to give

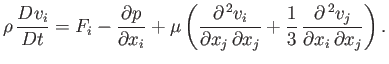$$\rho \,\frac{D v_i}{Dt}= F_i - \frac{\partial p}{\partial x_i} +\... ..._j}+ \frac{1}{3}\,\frac{\partial^{\,2} v_j}{\partial x_i\,\partial x_j}\right).$$ (1.55)

When expressed in vector form, the previous expression becomes

$$\rho\,\frac{D{\bf v}}{Dt}\equiv \rho\!\left[\frac{\partial {\bf v... ...\mu\left[\nabla^{\,2} {\bf v} + \frac{1}{3}\,\nabla(\nabla\cdot{\bf v})\right],$$ (1.56)

where use has been made of Equation (1.39). Here,

$$[({\bf a}\cdot\nabla){\bf b}]_i = a_j\,\frac{\partial b_i}{\partial x_j},$$ (1.57)

$$(\nabla^{\,2}{\bf v})_i = \nabla^{\,2} v_i.$$ (1.58)

Note, however, that the previous identities are only valid in Cartesian coordinates. (See Appendix C.)