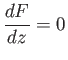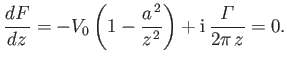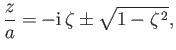Next: Method of Images
Up: Two-Dimensional Potential Flow
Previous: Complex Velocity Potential
Complex Velocity
Equations (5.17), (5.20), and (6.15) imply that
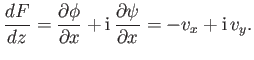 |
(6.35) |
Consequently, 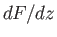 is termed the complex velocity. It follows that
is termed the complex velocity. It follows that
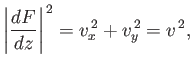 |
(6.36) |
where 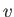 is the flow speed.
is the flow speed.
A stagnation point is defined as a point in a flow pattern at which the flow speed, 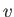 , falls to zero. (See Section 5.8.)
According to the previous expression,
, falls to zero. (See Section 5.8.)
According to the previous expression,
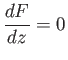 |
(6.37) |
at a stagnation point. For instance, the stagnation points of the flow pattern produced when a cylindrical obstacle of radius 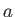 , centered on the origin, is placed in a uniform flow of speed
, centered on the origin, is placed in a uniform flow of speed 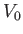 , directed parallel to the
, directed parallel to the  -axis, and the circulation of the flow around is cylinder is
-axis, and the circulation of the flow around is cylinder is
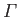 , are found by setting the derivative of the complex potential (6.32) to zero.
It follows that the stagnation points satisfy the quadratic equation
, are found by setting the derivative of the complex potential (6.32) to zero.
It follows that the stagnation points satisfy the quadratic equation
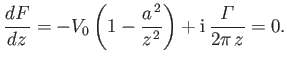 |
(6.38) |
The solutions are
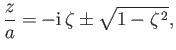 |
(6.39) |
where
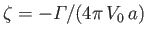 ,
with the proviso that
,
with the proviso that 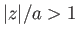 , because the region
, because the region 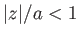 is occupied by the cylinder. Thus, if
is occupied by the cylinder. Thus, if
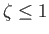 then there are two stagnation points on the surface of the cylinder at
then there are two stagnation points on the surface of the cylinder at
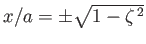 and
and
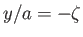 .
On the other hand, if
.
On the other hand, if 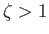 then there is a single stagnation point below the cylinder at
then there is a single stagnation point below the cylinder at 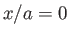 and
and
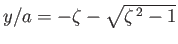 .
.
According to Section 4.15, Bernoulli's theorem in an steady, irrotational, incompressible fluid takes the form
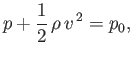 |
(6.40) |
where 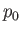 is a uniform constant. Here, gravity (and any other body force) has been neglected. Thus, the
pressure distribution in such a fluid can be written
is a uniform constant. Here, gravity (and any other body force) has been neglected. Thus, the
pressure distribution in such a fluid can be written
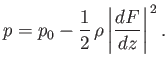 |
(6.41) |



Next: Method of Images
Up: Two-Dimensional Potential Flow
Previous: Complex Velocity Potential
Richard Fitzpatrick
2016-01-22
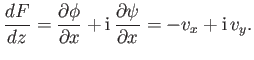
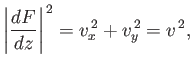
![]() , falls to zero. (See Section 5.8.)
According to the previous expression,
, falls to zero. (See Section 5.8.)
According to the previous expression,