Next: Exercises
Up: Incompressible Inviscid Flow
Previous: Kelvin Circulation Theorem
Irrotational Flow
Flow is said to be irrotational when the vorticity
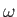 has the magnitude zero everywhere.
It immediately follows, from Equation (4.77), that the circulation around any arbitrary loop in an irrotational
flow pattern is zero (provided that the loop can be spanned by a surface that lies entirely within the fluid). Hence, from Kelvin's circulation theorem, if an inviscid fluid is initially irrotational
then it remains irrotational at all subsequent times. This can be seen more directly from the
equation of motion of an inviscid incompressible fluid which, according to Equations (1.39) and (1.79), takes the
form
has the magnitude zero everywhere.
It immediately follows, from Equation (4.77), that the circulation around any arbitrary loop in an irrotational
flow pattern is zero (provided that the loop can be spanned by a surface that lies entirely within the fluid). Hence, from Kelvin's circulation theorem, if an inviscid fluid is initially irrotational
then it remains irrotational at all subsequent times. This can be seen more directly from the
equation of motion of an inviscid incompressible fluid which, according to Equations (1.39) and (1.79), takes the
form
 |
(4.82) |
because  is a constant. However, from Equation (A.171),
is a constant. However, from Equation (A.171),
Thus, we obtain
Taking the curl of this equation, and making use of the vector identities
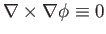 [see Equation (A.176)],
[see Equation (A.176)],
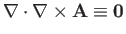 [see Equation (A.173)], as well as the identity (A.179), and the fact that
[see Equation (A.173)], as well as the identity (A.179), and the fact that
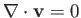 in an incompressible fluid, we obtain the vorticity evolution equation
in an incompressible fluid, we obtain the vorticity evolution equation
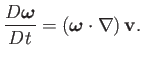 |
(4.85) |
Thus, if
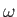
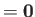 , initially, then
, initially, then
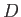
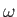
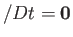 , and, consequently,
, and, consequently,
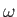
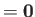 at all subsequent times.
at all subsequent times.
Suppose that 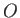 is a fixed point, and
is a fixed point, and 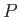 an arbitrary movable point, in an irrotational fluid. Let
an arbitrary movable point, in an irrotational fluid. Let 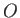 and
and 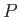 be joined
by two different paths,
be joined
by two different paths,  and
and 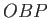 (say). It follows that
(say). It follows that 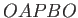 is a closed curve. Because the circulation
around such a curve in an irrotational fluid is zero, we can write
is a closed curve. Because the circulation
around such a curve in an irrotational fluid is zero, we can write
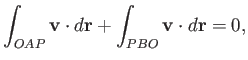 |
(4.86) |
which implies that
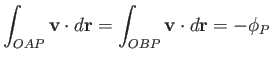 |
(4.87) |
(say). It is clear that 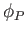 is a scalar function whose value depends on the
position of
is a scalar function whose value depends on the
position of 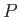 (and the fixed point
(and the fixed point 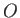 ), but not on the path taken between
), but not on the path taken between 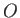 and
and 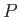 .
Thus, if
.
Thus, if 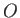 is the origin of our coordinate system, and
is the origin of our coordinate system, and 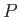 an arbitrary point whose position
vector is
an arbitrary point whose position
vector is  , then we have effectively defined a scalar field
, then we have effectively defined a scalar field
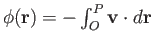 .
.
Consider a point 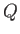 that is sufficiently close to
that is sufficiently close to 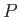 that the velocity
that the velocity  is constant along
is constant along 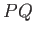 .
Let
.
Let
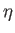 be the position vector of
be the position vector of 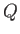 relative to
relative to 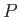 . It then follows that (see Section A.18)
. It then follows that (see Section A.18)
The previous equation becomes exact in the limit that
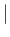
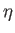
 . Because
. Because 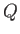 is arbitrary (provided that it is
sufficiently close to
is arbitrary (provided that it is
sufficiently close to 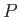 ), the
direction of the vector
), the
direction of the vector
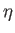 is also arbitrary, which implies that
is also arbitrary, which implies that
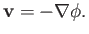 |
(4.89) |
We, thus, conclude that if the motion of a fluid is irrotational then the associated velocity field can always be expressed as minus the
gradient of a scalar function of position,
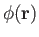 . This scalar function is called the velocity potential, and
flow which is derived from such a potential is known as potential flow. Note that the velocity potential
is undefined to an arbitrary additive constant.
. This scalar function is called the velocity potential, and
flow which is derived from such a potential is known as potential flow. Note that the velocity potential
is undefined to an arbitrary additive constant.
We have demonstrated that a velocity potential necessarily exists in a fluid whose velocity field is irrotational.
Conversely, when a velocity potential exists the flow is necessarily irrotational. This follows because [see Equation (A.176)]
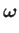  |
(4.90) |
Incidentally, the fluid velocity at any given point in an irrotational fluid is normal to the constant-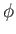 surface that
passes through that point.
surface that
passes through that point.
If a flow pattern is both irrotational and incompressible then we have
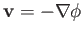 |
(4.91) |
and
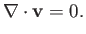 |
(4.92) |
These two expressions can be combined to give (see Section A.21)
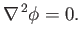 |
(4.93) |
In other words, the velocity potential in an incompressible irrotational fluid satisfies Laplace's equation.
According to Equation (4.84), if the flow pattern in an incompressible inviscid fluid is also irrotational, so that
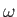
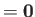 and
and
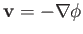 , then we can write
, then we can write
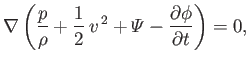 |
(4.94) |
which implies that
 |
(4.95) |
where 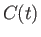 is uniform in space, but can vary in time. In fact, the time variation of
is uniform in space, but can vary in time. In fact, the time variation of 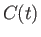 can be eliminated
by adding the appropriate function of time (but not of space) to the velocity potential,
can be eliminated
by adding the appropriate function of time (but not of space) to the velocity potential, 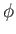 . Note that such
a procedure does not modify the instantaneous velocity field
. Note that such
a procedure does not modify the instantaneous velocity field  derived from
derived from 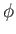 . Thus, the previous equation can
be rewritten
. Thus, the previous equation can
be rewritten
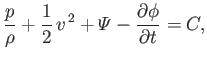 |
(4.96) |
where 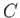 is constant in both space and time. Expression (4.96) is a generalization of Bernoulli's theorem (see Section 4.3)
that takes non-steady flow into account. However, this generalization is only valid for irrotational flow. For the special
case of steady flow, we get
is constant in both space and time. Expression (4.96) is a generalization of Bernoulli's theorem (see Section 4.3)
that takes non-steady flow into account. However, this generalization is only valid for irrotational flow. For the special
case of steady flow, we get
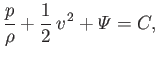 |
(4.97) |
which demonstrates that for steady irrotational flow the constant in Bernoulli's theorem is the same on all streamlines. (See Section 4.3.)



Next: Exercises
Up: Incompressible Inviscid Flow
Previous: Kelvin Circulation Theorem
Richard Fitzpatrick
2016-01-22


![]() is a fixed point, and
is a fixed point, and ![]() an arbitrary movable point, in an irrotational fluid. Let
an arbitrary movable point, in an irrotational fluid. Let ![]() and
and ![]() be joined
by two different paths,
be joined
by two different paths, ![]() and
and ![]() (say). It follows that
(say). It follows that ![]() is a closed curve. Because the circulation
around such a curve in an irrotational fluid is zero, we can write
is a closed curve. Because the circulation
around such a curve in an irrotational fluid is zero, we can write
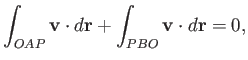
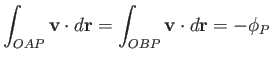
![]() that is sufficiently close to
that is sufficiently close to ![]() that the velocity
that the velocity ![]() is constant along
is constant along ![]() .
Let
.
Let
![]() be the position vector of
be the position vector of ![]() relative to
relative to ![]() . It then follows that (see Section A.18)
. It then follows that (see Section A.18)

![]()
![]() and
and
![]() , then we can write
, then we can write