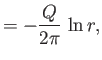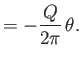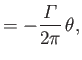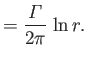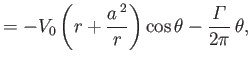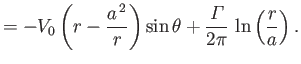Next: Complex Velocity
Up: Two-Dimensional Potential Flow
Previous: Cauchy-Riemann Relations
Complex Velocity Potential
Equations (6.17)-(6.18) are identical to Equations (5.21)-(5.22).
This suggests that the real and imaginary parts of a well-behaved function of the complex variable
can be interpreted as the velocity potential and stream function, respectively, of some two-dimensional,
irrotational, incompressible flow pattern.
For instance,
suppose that
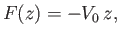 |
(6.23) |
where 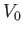 is real. It
follows that
is real. It
follows that
It can be seen, by comparison with the analysis of Section 5.4, that the complex velocity potential (6.23) corresponds to uniform flow of speed 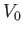 directed along the
directed along the  -axis. Furthermore, as is
easily demonstrated, the complex velocity potential associated with uniform flow of speed
-axis. Furthermore, as is
easily demonstrated, the complex velocity potential associated with uniform flow of speed 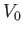 whose
direction subtends a (counter-clockwise) angle
whose
direction subtends a (counter-clockwise) angle 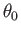 with the
with the  -axis is
-axis is
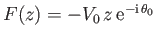 .
.
Suppose that
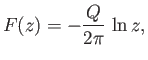 |
(6.26) |
where 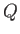 is real.
Because
is real.
Because
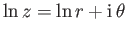 (Riley 1974), it follows that
(Riley 1974), it follows that
Thus, according to the analysis of Section 5.5, the complex velocity potential (6.26) corresponds
to the flow pattern of a line source, of strength 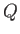 , located at the origin. (See Figure 5.3.)
As a simple generalization of this result, the complex potential of a line source, of strength
, located at the origin. (See Figure 5.3.)
As a simple generalization of this result, the complex potential of a line source, of strength 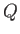 , located at the point
, located at the point 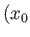 ,
, 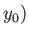 , is
, is
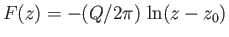 , where
, where
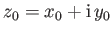 .
It can be seen, from Equation (6.26), that the complex velocity potential of a line source is singular at the
location of the source.
.
It can be seen, from Equation (6.26), that the complex velocity potential of a line source is singular at the
location of the source.
Suppose that
 |
(6.29) |
where
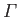 is real. It follows that
is real. It follows that
Thus, according to the analysis of Section 5.6, the complex velocity potential (6.29) corresponds
to the flow pattern of a vortex filament of intensity
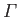 located at the origin. (See Figure 5.5.)
As a simple generalization of this result, the complex potential of a vortex filament, of intensity
located at the origin. (See Figure 5.5.)
As a simple generalization of this result, the complex potential of a vortex filament, of intensity
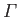 , located at the point
, located at the point 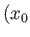 ,
, 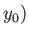 , is
, is
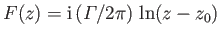 , where
, where
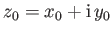 .
According to Equation (6.29), the complex velocity potential of a vortex filament is singular at the
location of the filament.
.
According to Equation (6.29), the complex velocity potential of a vortex filament is singular at the
location of the filament.
Suppose, finally, that
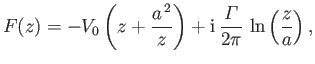 |
(6.32) |
where 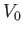 ,
, 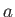 , and
, and
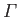 , are real. It follows that
, are real. It follows that
Thus, according to the analysis of Section 5.8, the complex velocity potential (6.32) corresponds to uniform
flow of unperturbed speed 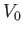 , running parallel to the
, running parallel to the  -axis, around an impenetrable circular cylinder of radius
-axis, around an impenetrable circular cylinder of radius 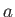 , centered on the origin. (See Figures 5.6, 5.7, and 5.8.) Here,
, centered on the origin. (See Figures 5.6, 5.7, and 5.8.) Here,
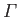 is the circulation of the flow about the cylinder. It can be seen that
is the circulation of the flow about the cylinder. It can be seen that  on the surface of the cylinder (
on the surface of the cylinder ( ), which ensures that the normal velocity is zero on this surface (because the surface corresponds to a streamline), as must be the case if the
cylinder is impenetrable.
), which ensures that the normal velocity is zero on this surface (because the surface corresponds to a streamline), as must be the case if the
cylinder is impenetrable.



Next: Complex Velocity
Up: Two-Dimensional Potential Flow
Previous: Cauchy-Riemann Relations
Richard Fitzpatrick
2016-01-22