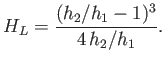Next: Tidal Bores
Up: Incompressible Inviscid Flow
Previous: Flow over Shallow Bump
Under certain circumstances, water flowing within a horizontal open channel (i.e., a stream) of constant width
is found to have a depth that changes very rapidly over a short section of the channel. This
phenomenon is known as a hydraulic jump, and is illustrated in Figure 4.6.
Figure 4.6:
A hydraulic jump.
 |
Suppose that the jump is stationary.
Let 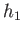 ,
, 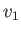 , and
, and 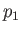 be the depth, flow velocity, and pressure, of the water, respectively, upstream of the jump.
Similarly let
be the depth, flow velocity, and pressure, of the water, respectively, upstream of the jump.
Similarly let  ,
, 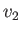 , and
, and  , be the depth, flow velocity and pressure, respectively, downstream of the jump.
As before,
, be the depth, flow velocity and pressure, respectively, downstream of the jump.
As before, 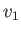 and
and 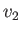 are assumed to be uniform across the channel. We are also assuming that the flow is laminar
(i.e., smooth) both upstream and downstream of the jump.
Note that the region of the channel in which the
jump occurs is generally associated with violent mixing that gives rise to significant
transfer of mechanical energy from the laminar (i.e., smooth) to the turbulent component of the flow. (The latter component is localized in the vicinity of the jump, and
is continuously dissipated by viscosity on small-scales.) Consequently, we cannot use Bernoulli's equation to analyze the jump, because this
equation assumes that the laminar component of the flow conserves mechanical energy. However, we can still make
use of fluid continuity, as well as the Euler momentum theorem, neither of which depend on the conservation of
mechanical energy.
are assumed to be uniform across the channel. We are also assuming that the flow is laminar
(i.e., smooth) both upstream and downstream of the jump.
Note that the region of the channel in which the
jump occurs is generally associated with violent mixing that gives rise to significant
transfer of mechanical energy from the laminar (i.e., smooth) to the turbulent component of the flow. (The latter component is localized in the vicinity of the jump, and
is continuously dissipated by viscosity on small-scales.) Consequently, we cannot use Bernoulli's equation to analyze the jump, because this
equation assumes that the laminar component of the flow conserves mechanical energy. However, we can still make
use of fluid continuity, as well as the Euler momentum theorem, neither of which depend on the conservation of
mechanical energy.
Fluid continuity yields
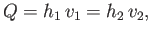 |
(4.37) |
where 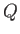 is the fixed flow rate per unit width. Furthermore, the Euler momentum theorem (see Section 4.4) implies that
is the fixed flow rate per unit width. Furthermore, the Euler momentum theorem (see Section 4.4) implies that
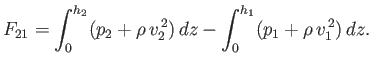 |
(4.38) |
Here,  is the horizontal thrust per unit width exerted by the channel bed on the water lying between points
is the horizontal thrust per unit width exerted by the channel bed on the water lying between points  and
and  .
Moreover,
.
Moreover,  measured vertical height above the bed. Assuming the usual linear pressure variation with depth,
we can write
measured vertical height above the bed. Assuming the usual linear pressure variation with depth,
we can write
where 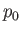 is atmospheric pressure.
Hence, we deduce that
is atmospheric pressure.
Hence, we deduce that
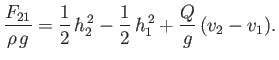 |
(4.41) |
The neglect of frictional drag at the channel bed implies that 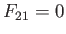 . Thus, we obtain
. Thus, we obtain
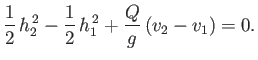 |
(4.42) |
The previous equation possesses the trivial solution 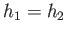 and
and  , which corresponds to the absence of a
hydraulic jump. Eliminating
, which corresponds to the absence of a
hydraulic jump. Eliminating 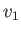 and
and 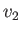 between Equations (4.37) and (4.42), and canceling
a common factor
between Equations (4.37) and (4.42), and canceling
a common factor 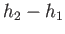 , we obtain the non-trivial solution
, we obtain the non-trivial solution
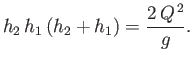 |
(4.43) |
Now, the upstream Froude number is defined
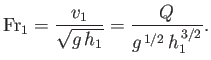 |
(4.44) |
Eliminating 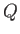 between the previous two equations, we obtain
between the previous two equations, we obtain
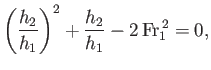 |
(4.45) |
which can be solved to give
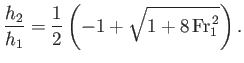 |
(4.46) |
Here, we have neglected an unphysical solution in which 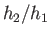 is negative.
Note that
is negative.
Note that
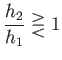 |
|
as |
|
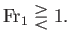 |
(4.47) |
The downstream Froude number is defined
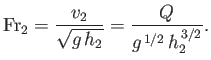 |
(4.48) |
Eliminating 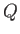 between Equations (4.43) and (4.48), we obtain
between Equations (4.43) and (4.48), we obtain
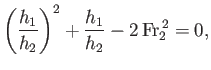 |
(4.49) |
which can be solved to give
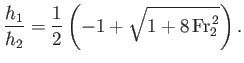 |
(4.50) |
Here, we have again neglected an unphysical solution in which 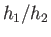 is negative.
We can combine Equations (4.46) and (4.50) to give
is negative.
We can combine Equations (4.46) and (4.50) to give
 |
(4.51) |
where
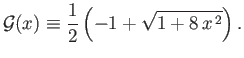 |
(4.52) |
Note that
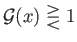 |
|
as |
|
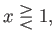 |
(4.53) |
which implies that
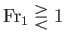 |
|
as |
|
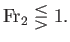 |
(4.54) |
In other words, if the upstream flow is super-critical then the downstream flow is sub-critical, and 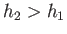 .
On the other hand, if the upstream flow is sub-critical then the downstream flow is super-critical, and
.
On the other hand, if the upstream flow is sub-critical then the downstream flow is super-critical, and 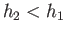 .
.
By analogy with Equation (4.18), we can define the head heights of the flows upstream and downstream of the jump as
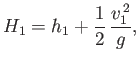 |
(4.55) |
and
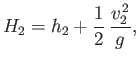 |
(4.56) |
respectively.
Of course, in the absence of any transfer of mechanical energy from the laminar to the turbulent component of the flow, within the jump, we
would expect 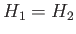 . (Because this is what Bernoulli's equation predicts.) In the presence of the transfer, we expect
. (Because this is what Bernoulli's equation predicts.) In the presence of the transfer, we expect 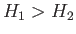 .
In other words, we expect there to be a head loss across the jump. Note that it is impossible for
.
In other words, we expect there to be a head loss across the jump. Note that it is impossible for 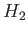 to exceed
to exceed 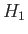 , because this would
imply a transfer of mechanical energy from the turbulent to the laminar component of the flow, within the jump, which violates the second
law of thermodynamics.
Let
, because this would
imply a transfer of mechanical energy from the turbulent to the laminar component of the flow, within the jump, which violates the second
law of thermodynamics.
Let
 |
(4.57) |
be the positive definite head loss.
Making use of some previous definitions, we can write
 |
(4.58) |
Now, according to Equation (4.45),
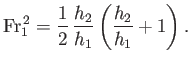 |
(4.59) |
Hence, combining the previous two equations, we obtain
![$\displaystyle H_L = \frac{1}{4}\frac{h_1}{h_2}\left(\frac{h_2}{h_1}-1\right)\left[-4\,\frac{h_2}{h_1}+ \left(\frac{h_2}{h_1}+1\right)^2\right],$](img1506.png) |
(4.60) |
or
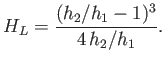 |
(4.61) |
Thus, the thermodynamic constraint 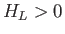 implies that
implies that 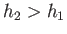 . However, as we have already seen,
. However, as we have already seen, 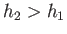 implies that
implies that
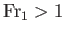 .
In other words, a stationary hydraulic jump can only occur when the upstream flow is super-critical, and the downstream flow sub-critical.
.
In other words, a stationary hydraulic jump can only occur when the upstream flow is super-critical, and the downstream flow sub-critical.
A hydraulic jump often occurs at the base of a spillway from a dam, where the flow is accelerated to super-critical
speeds. Because a hydraulic jump always results in a loss of mechanical energy from the flow, spillways
are sometimes designed to promote jumps, so as to deliberately remove energy from the flow, thereby reducing the
danger from excessive currents in flood control.



Next: Tidal Bores
Up: Incompressible Inviscid Flow
Previous: Flow over Shallow Bump
Richard Fitzpatrick
2016-01-22

![]() ,
, ![]() , and
, and ![]() be the depth, flow velocity, and pressure, of the water, respectively, upstream of the jump.
Similarly let
be the depth, flow velocity, and pressure, of the water, respectively, upstream of the jump.
Similarly let ![]() ,
, ![]() , and
, and ![]() , be the depth, flow velocity and pressure, respectively, downstream of the jump.
As before,
, be the depth, flow velocity and pressure, respectively, downstream of the jump.
As before, ![]() and
and ![]() are assumed to be uniform across the channel. We are also assuming that the flow is laminar
(i.e., smooth) both upstream and downstream of the jump.
Note that the region of the channel in which the
jump occurs is generally associated with violent mixing that gives rise to significant
transfer of mechanical energy from the laminar (i.e., smooth) to the turbulent component of the flow. (The latter component is localized in the vicinity of the jump, and
is continuously dissipated by viscosity on small-scales.) Consequently, we cannot use Bernoulli's equation to analyze the jump, because this
equation assumes that the laminar component of the flow conserves mechanical energy. However, we can still make
use of fluid continuity, as well as the Euler momentum theorem, neither of which depend on the conservation of
mechanical energy.
are assumed to be uniform across the channel. We are also assuming that the flow is laminar
(i.e., smooth) both upstream and downstream of the jump.
Note that the region of the channel in which the
jump occurs is generally associated with violent mixing that gives rise to significant
transfer of mechanical energy from the laminar (i.e., smooth) to the turbulent component of the flow. (The latter component is localized in the vicinity of the jump, and
is continuously dissipated by viscosity on small-scales.) Consequently, we cannot use Bernoulli's equation to analyze the jump, because this
equation assumes that the laminar component of the flow conserves mechanical energy. However, we can still make
use of fluid continuity, as well as the Euler momentum theorem, neither of which depend on the conservation of
mechanical energy.
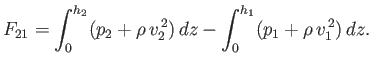
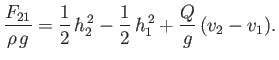
![]() and
and ![]() , which corresponds to the absence of a
hydraulic jump. Eliminating
, which corresponds to the absence of a
hydraulic jump. Eliminating ![]() and
and ![]() between Equations (4.37) and (4.42), and canceling
a common factor
between Equations (4.37) and (4.42), and canceling
a common factor ![]() , we obtain the non-trivial solution
, we obtain the non-trivial solution
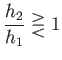
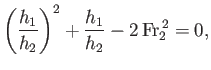
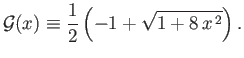
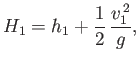
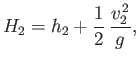


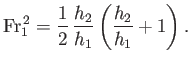
![$\displaystyle H_L = \frac{1}{4}\frac{h_1}{h_2}\left(\frac{h_2}{h_1}-1\right)\left[-4\,\frac{h_2}{h_1}+ \left(\frac{h_2}{h_1}+1\right)^2\right],$](img1506.png)