


Next: Stationary Hydraulic Jumps
Up: Incompressible Inviscid Flow
Previous: Sub-Critical and Super-Critical Flow
Figure 4.5:
Flow over a shallow bump.
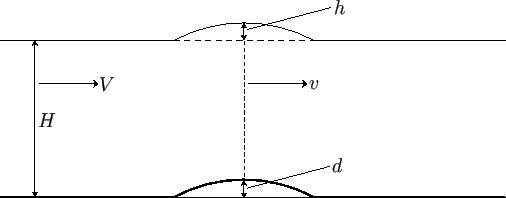 |
Consider a shallow stream of depth 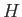 , uniform width, and uniform flow velocity
, uniform width, and uniform flow velocity  . Suppose that there is
a very shallow bump of height
. Suppose that there is
a very shallow bump of height 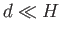 on the (horizontal) bed of the stream, as shown in Figure 4.5. Suppose, further, that,
at the point where the stream passes over the top of the bump, its velocity is
on the (horizontal) bed of the stream, as shown in Figure 4.5. Suppose, further, that,
at the point where the stream passes over the top of the bump, its velocity is 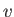 , and its surface rises a height
, and its surface rises a height 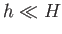 above the unperturbed
surface.
above the unperturbed
surface.
Fluid continuity yields
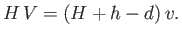 |
(4.29) |
Furthermore, application of Bernoulli's equation to a streamline lying on the surface of the water (where the pressure is
atmospheric) gives
 |
(4.30) |
The previous equation reduces to
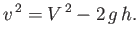 |
(4.31) |
Eliminating 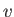 between Equations (4.29) and (4.31), we obtain
between Equations (4.29) and (4.31), we obtain
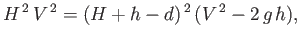 |
(4.32) |
which can be rearranged to give
![$\displaystyle V^{\,2}\left[(H+h-d)^2-H^{\,2}\right]=2\,g\,h\,(H+h-d)^2,$](img1458.png) |
(4.33) |
or
![$\displaystyle {\rm Fr}^{\,2}\left[\left(1+\frac{h-d}{H}\right)^2-1\right] = 2\,\frac{h}{H}\left(1+\frac{h-d}{H}\right)^{\,2}.$](img1459.png) |
(4.34) |
Here,
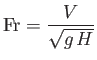 |
(4.35) |
is the Froude number of the unperturbed flow. Finally, given that 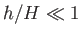 and
and 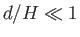 , Equation (4.34) reduces to
, Equation (4.34) reduces to
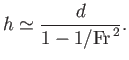 |
(4.36) |
It follows, from the previous expression, that if the flow is super-critical, so that
 , then
, then  is positive.
On the other hand, if the flow is sub-critical, so that
is positive.
On the other hand, if the flow is sub-critical, so that
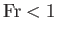 , then
, then  is negative. Thus, if a
super-critical shallow stream passes over a very shallow bump on its bed then the surface of the stream becomes slightly elevated. On the other hand, if
a sub-critical stream passes over such a bump then the surface of the stream becomes slightly depressed. A similar
effect occurs when there is a narrowing of the channel in the horizontal direction. A more sophisticated version of the
previous calculation, which does not necessarily assume that the stream is shallow, can be found in Section 11.10.
is negative. Thus, if a
super-critical shallow stream passes over a very shallow bump on its bed then the surface of the stream becomes slightly elevated. On the other hand, if
a sub-critical stream passes over such a bump then the surface of the stream becomes slightly depressed. A similar
effect occurs when there is a narrowing of the channel in the horizontal direction. A more sophisticated version of the
previous calculation, which does not necessarily assume that the stream is shallow, can be found in Section 11.10.



Next: Stationary Hydraulic Jumps
Up: Incompressible Inviscid Flow
Previous: Sub-Critical and Super-Critical Flow
Richard Fitzpatrick
2016-01-22

![]() , uniform width, and uniform flow velocity
, uniform width, and uniform flow velocity ![]() . Suppose that there is
a very shallow bump of height
. Suppose that there is
a very shallow bump of height ![]() on the (horizontal) bed of the stream, as shown in Figure 4.5. Suppose, further, that,
at the point where the stream passes over the top of the bump, its velocity is
on the (horizontal) bed of the stream, as shown in Figure 4.5. Suppose, further, that,
at the point where the stream passes over the top of the bump, its velocity is ![]() , and its surface rises a height
, and its surface rises a height ![]() above the unperturbed
surface.
above the unperturbed
surface.

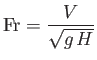
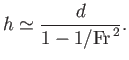
![]() , then
, then ![]() is positive.
On the other hand, if the flow is sub-critical, so that
is positive.
On the other hand, if the flow is sub-critical, so that
![]() , then
, then ![]() is negative. Thus, if a
super-critical shallow stream passes over a very shallow bump on its bed then the surface of the stream becomes slightly elevated. On the other hand, if
a sub-critical stream passes over such a bump then the surface of the stream becomes slightly depressed. A similar
effect occurs when there is a narrowing of the channel in the horizontal direction. A more sophisticated version of the
previous calculation, which does not necessarily assume that the stream is shallow, can be found in Section 11.10.
is negative. Thus, if a
super-critical shallow stream passes over a very shallow bump on its bed then the surface of the stream becomes slightly elevated. On the other hand, if
a sub-critical stream passes over such a bump then the surface of the stream becomes slightly depressed. A similar
effect occurs when there is a narrowing of the channel in the horizontal direction. A more sophisticated version of the
previous calculation, which does not necessarily assume that the stream is shallow, can be found in Section 11.10.