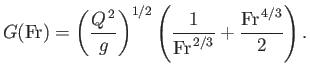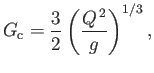Next: Flow over Shallow Bump
Up: Incompressible Inviscid Flow
Previous: Flow Through an Orifice
Sub-Critical and Super-Critical Flow
Consider a shallow stream of depth  , uniform width, and uniform flow velocity
, uniform width, and uniform flow velocity 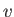 , that is fed from a deep
reservoir whose surface lies a height
, that is fed from a deep
reservoir whose surface lies a height 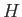 above the (horizontal) bed of the stream. Here,
above the (horizontal) bed of the stream. Here, 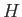 is usually
referred to as the head height. Assuming that the
water in the reservoir is effectively stationary, application of Bernoulli's equation to a streamline
lying on the surface of the water (where the pressure is atmospheric) yields
is usually
referred to as the head height. Assuming that the
water in the reservoir is effectively stationary, application of Bernoulli's equation to a streamline
lying on the surface of the water (where the pressure is atmospheric) yields
 |
(4.18) |
Let 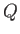 be the flow rate per unit width of the stream, which is assumed to be fixed. It follows that
be the flow rate per unit width of the stream, which is assumed to be fixed. It follows that
 |
(4.19) |
The previous two equations can be combined to give
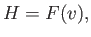 |
(4.20) |
where
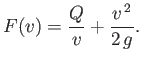 |
(4.21) |
It is easily demonstrated that the function 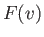 attains its minimum value,
attains its minimum value,
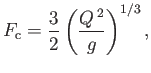 |
(4.22) |
when 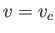 , where
, where
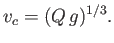 |
(4.23) |
We conclude that, as long as
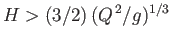 , Equation (4.20) possesses two
possible solutions that are consistent with a given head height and flow rate. In one solution, the stream flows at a relatively slow velocity,
, Equation (4.20) possesses two
possible solutions that are consistent with a given head height and flow rate. In one solution, the stream flows at a relatively slow velocity, 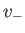 , which is such that
, which is such that 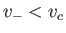 .
In the other, the stream flows at a relatively fast velocity,
.
In the other, the stream flows at a relatively fast velocity, 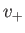 , which is such that
, which is such that 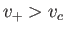 . The corresponding
depths are
. The corresponding
depths are
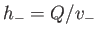 and
and
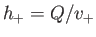 , respectively.
, respectively.
It is helpful to introduce the dimensionless Froude number,
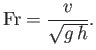 |
(4.24) |
(See Section 1.15.) Note that
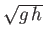 is the characteristic propagation velocity of a gravity wave in shallow water of depth
is the characteristic propagation velocity of a gravity wave in shallow water of depth  . (See Section 11.4.) Hence, if
. (See Section 11.4.) Hence, if
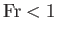 then the stream's flow velocity falls below the wave speed--such
flow is termed sub-critical. On the other hand, if
then the stream's flow velocity falls below the wave speed--such
flow is termed sub-critical. On the other hand, if
 then the flow velocity exceeds the wave speed--such flow is termed super-critical.
then the flow velocity exceeds the wave speed--such flow is termed super-critical.
We can combine Equations (4.18), (4.19), and (4.24) to give
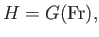 |
(4.25) |
where
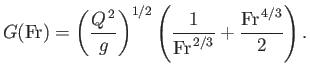 |
(4.26) |
It is easily demonstrated that
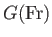 attains its minimum value
attains its minimum value
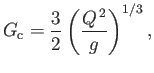 |
(4.27) |
when
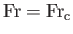 ,
where
,
where
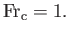 |
(4.28) |
Hence, we again conclude that, as long as
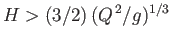 , there are two possible flow velocities of the
stream (parameterized by two different Froude numbers) that are consistent with a given head height and flow rate. However, it is now clear that the smaller velocity is
sub-critical (i.e.,
, there are two possible flow velocities of the
stream (parameterized by two different Froude numbers) that are consistent with a given head height and flow rate. However, it is now clear that the smaller velocity is
sub-critical (i.e.,
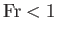 ), whereas the larger velocity is super-critical (i.e.,
), whereas the larger velocity is super-critical (i.e.,
 ).
).



Next: Flow over Shallow Bump
Up: Incompressible Inviscid Flow
Previous: Flow Through an Orifice
Richard Fitzpatrick
2016-01-22