


Next: Exercises
Up: Surface Tension
Previous: Capillary Curves
Axisymmetric Soap-Bubbles
Consider an axisymmetric soap-bubble whose surface takes the form 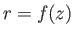 in cylindrical coordinates. (See Section C.3.) The
unit normal to the surface is
in cylindrical coordinates. (See Section C.3.) The
unit normal to the surface is
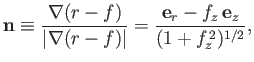 |
(3.55) |
where
 . Hence, from Equation (C.39), the mean curvature of the surface is given by
. Hence, from Equation (C.39), the mean curvature of the surface is given by
![$\displaystyle \nabla\cdot {\bf n} = \frac{1}{f\,f_z}\,\frac{d}{dz}\!\left[\frac{f}{(1+f_z^{\,2})^{1/2}}\right].$](img1235.png) |
(3.56) |
The Young-Laplace equation, (3.12), then yields
![$\displaystyle \frac{f\,f_z}{a} = \frac{d}{dz}\!\left[\frac{f}{(1+f_z^{\,2})^{1/2}}\right],$](img1236.png) |
(3.57) |
where
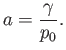 |
(3.58) |
Here, 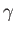 is the net surface tension, including the contributions from the internal and external soap/air interfaces. Moreover,
is the net surface tension, including the contributions from the internal and external soap/air interfaces. Moreover,
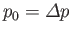 is the pressure difference between the interior and the exterior of the bubble. Equation (3.57)
can be integrated to give
is the pressure difference between the interior and the exterior of the bubble. Equation (3.57)
can be integrated to give
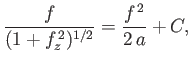 |
(3.59) |
where 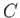 is a constant.
is a constant.
Suppose that the bubble occupies the region
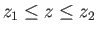 , where
, where 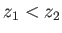 , and has a fixed
radius at its two end-points,
, and has a fixed
radius at its two end-points, 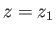 and
and  .
This could most easily be achieved by supporting the
bubble on two rigid parallel co-axial rings located at
.
This could most easily be achieved by supporting the
bubble on two rigid parallel co-axial rings located at 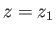 and
and  .
The net free energy required to create the bubble can be written
.
The net free energy required to create the bubble can be written
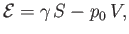 |
(3.60) |
where  is area of the bubble surface, and
is area of the bubble surface, and  the enclosed volume. The first term on the right-hand side of
the previous expression represents the work needed to overcome surface tension, whereas the second term
represents the work required to overcome the pressure difference,
the enclosed volume. The first term on the right-hand side of
the previous expression represents the work needed to overcome surface tension, whereas the second term
represents the work required to overcome the pressure difference, 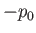 , between the exterior and
the interior of the bubble. From the general principles of statics, we expect a stable equilibrium state
of a mechanical system to be such as to minimize the net free energy, subject to any dynamical
constraints (Fitzpatrick 2012). It follows that the equilibrium shape of the bubble
is such as to minimize
, between the exterior and
the interior of the bubble. From the general principles of statics, we expect a stable equilibrium state
of a mechanical system to be such as to minimize the net free energy, subject to any dynamical
constraints (Fitzpatrick 2012). It follows that the equilibrium shape of the bubble
is such as to minimize
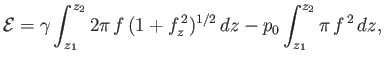 |
(3.61) |
subject to the constraint that the bubble radius, 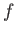 , be fixed at
, be fixed at 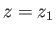 and
and  .
Hence, we need to find the function
.
Hence, we need to find the function 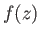 that minimizes the integral
that minimizes the integral
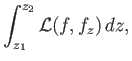 |
(3.62) |
where
 |
(3.63) |
subject to the constraint that 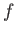 is fixed at the limits. This is a standard problem in the calculus of
variations. (See Appendix E.) In fact, because the functional
is fixed at the limits. This is a standard problem in the calculus of
variations. (See Appendix E.) In fact, because the functional
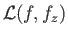 does not depend explicitly
on
does not depend explicitly
on  , the minimizing function is the solution of [see Equation (E.14)]
, the minimizing function is the solution of [see Equation (E.14)]
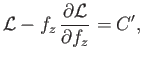 |
(3.64) |
where 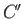 is an arbitrary constant.
Thus, we obtain
is an arbitrary constant.
Thus, we obtain
![$\displaystyle 2\pi\,\gamma\left[\frac{f}{(1+f_z^{\,2})^{1/2}}-\frac{f^{\,2}}{2\,a}\right] = C',$](img1252.png) |
(3.65) |
which can be rearranged to give Equation (3.59). Hence, we conclude that application of the Young-Laplace
equation does indeed lead to a bubble shape that minimizes the net free energy of the soap/air interfaces.
Consider the case 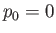 , in which there is no pressure difference across the surface of the bubble.
In this situation, writing
, in which there is no pressure difference across the surface of the bubble.
In this situation, writing
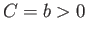 , Equation (3.59) reduces to
, Equation (3.59) reduces to
 |
(3.66) |
Moreover, according to the previous discussion, the bubble shape specified by Equation (3.66) is such as to minimize the surface area of the bubble (because the only contribution to the free energy of the soap/air interfaces is directly proportional
to the bubble area).
The previous equation can be rearranged to give
 |
(3.67) |
which leads to
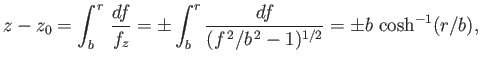 |
(3.68) |
or
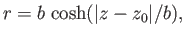 |
(3.69) |
where 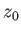 is a constant.
This expression describes an axisymmetric surface known as a catenoid.
is a constant.
This expression describes an axisymmetric surface known as a catenoid.
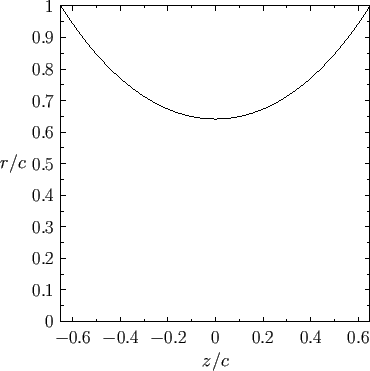
Figure:
Radius versus axial distance for a catenoid soap bubble supported by two parallel co-axial rings
of radius 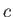 located at
located at
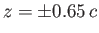 .
.
 |
Suppose, for instance, that the soap bubble is
supported by identical rings of radius 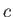 that are located a perpendicular
distance
that are located a perpendicular
distance 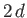 apart. Without loss of generality, we can specify that the rings lie at
apart. Without loss of generality, we can specify that the rings lie at  . It follows,
from Equation (3.69), that
. It follows,
from Equation (3.69), that  , and
, and
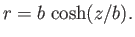 |
(3.70) |
Here, the parameter  must be chosen so as to satisfy
must be chosen so as to satisfy
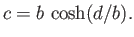 |
(3.71) |
For example, if 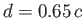 then
then
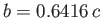 , and the resulting bubble shape is illustrated in Figure 3.7.
, and the resulting bubble shape is illustrated in Figure 3.7.
Let 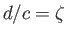 and
and 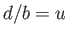 , in which case the previous equation becomes
, in which case the previous equation becomes
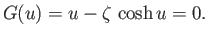 |
(3.72) |
Now, the function 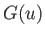 attains a maximum value
attains a maximum value
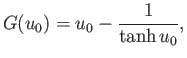 |
(3.73) |
when
 . Moreover, if
. Moreover, if 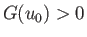 then Equation (3.72) possesses two roots. It turns
out that the root associated with the smaller value of
then Equation (3.72) possesses two roots. It turns
out that the root associated with the smaller value of  minimizes the interface system energy, whereas
the other root maximizes the free energy. Hence, the former root corresponds to a stable
equilibrium state, whereas the latter corresponds to an unstable
equilibrium state. On the other hand, if
minimizes the interface system energy, whereas
the other root maximizes the free energy. Hence, the former root corresponds to a stable
equilibrium state, whereas the latter corresponds to an unstable
equilibrium state. On the other hand, if 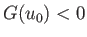 then Equation (3.72)
possesses no roots, implying the absence of any equilibrium state. The critical case
then Equation (3.72)
possesses no roots, implying the absence of any equilibrium state. The critical case 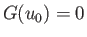 corresponds to
corresponds to  and
and
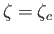 , where
, where
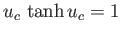 and
and
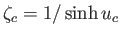 .
It is easily demonstrated that
.
It is easily demonstrated that
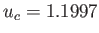 and
and
 .
We conclude that a stable equilibrium state of a catenoid bubble only exists when
.
We conclude that a stable equilibrium state of a catenoid bubble only exists when
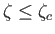 , which corresponds to
, which corresponds to
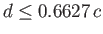 . If the relative ring spacing
. If the relative ring spacing 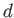 exceeds the critical value
exceeds the critical value 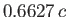 then the bubble presumably bursts.
then the bubble presumably bursts.
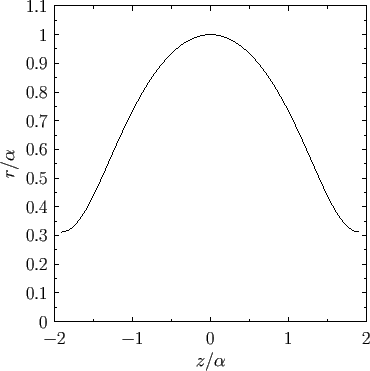
Figure:
Radius versus axial distance for an unduloid soap bubble calculated with 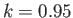 .
.
 |
Consider the case 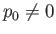 , in which there is a pressure difference across the surface of the bubble.
In this situation, writing
, in which there is a pressure difference across the surface of the bubble.
In this situation, writing
Equation (3.59) becomes
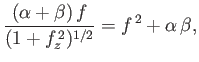 |
(3.76) |
which can be rearranged to give
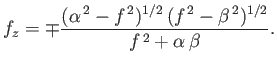 |
(3.77) |
We can assume, without loss of generality, that
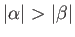 .
It follows, from the previous expression,
that
.
It follows, from the previous expression,
that
 . Hence, we can write
. Hence, we can write
where
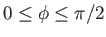 and
and
 .
It follows that
.
It follows that
and
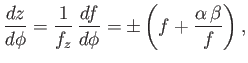 |
(3.82) |
which can be integrated to give
![$\displaystyle \vert z\vert= \vert\alpha\vert\left[E(\phi,k) + {\rm sgn}(\alpha\,\beta)\,(1-k^{\,2})^{1/2}\,F(\phi,k)\right],$](img1308.png) |
(3.83) |
where 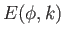 and
and 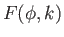 are incomplete elliptic integrals [see Equations (3.40)
and (3.41)]. Here, we have assumed that
are incomplete elliptic integrals [see Equations (3.40)
and (3.41)]. Here, we have assumed that 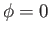 when
when  .
There are three cases of interest.
.
There are three cases of interest.
Figure:
Radius versus axial distance for a positive pressure nodoid soap bubble calculated with 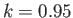 .
.
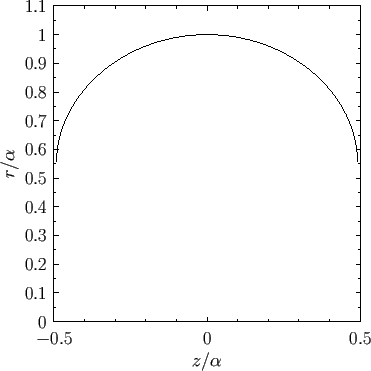 |
In the first case,  and
and  . It follows that
. It follows that
 for
for
 , and
, and
 for
for
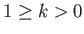 , where
, where
The axisymmetric curve parameterized by the previous pair of equations is known as an unduloid. Note that an
unduloid bubble always has positive internal pressure (relative to the external pressure): that is, 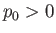 .
An example unduloid soap bubble is illustrated in Figure 3.8
.
An example unduloid soap bubble is illustrated in Figure 3.8
In the second case, 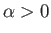 and
and  . It follows that
. It follows that
 for
for
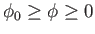 , and
, and
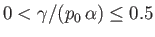 for
for
 , where
, where
![$ \phi_0= \sin^{-1}([1-(1-k^{\,2})^{1/2}]^{1/2}/k)$](img1327.png) , and
, and
The axisymmetric curve parameterized by the previous pair of equations is known as an nodoid. This
particular type of nodoid bubble has positive internal pressure: that is, 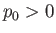 .
An example positive pressure nodoid soap bubble is illustrated in Figure 3.9.
.
An example positive pressure nodoid soap bubble is illustrated in Figure 3.9.
In the third case,  and
and  . It follows that
. It follows that
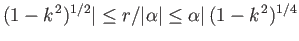 for
for
 (or
(or
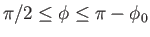 ), and
), and
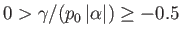 for
for
 , where
, where
The axisymmetric curve parameterized by the previous pair of equations is again a nodoid. However, this
particular type of nodoid bubble has negative internal pressure: that is, 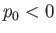 .
An example negative pressure nodoid soap bubble is illustrated in Figure 3.10.
.
An example negative pressure nodoid soap bubble is illustrated in Figure 3.10.
Figure:
Radius versus axial distance for a negative pressure nodoid soap bubble calculated with 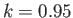 .
.
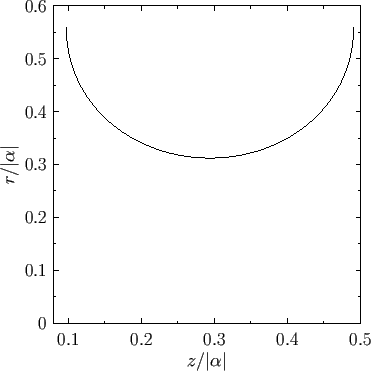 |



Next: Exercises
Up: Surface Tension
Previous: Capillary Curves
Richard Fitzpatrick
2016-01-22
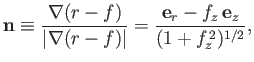
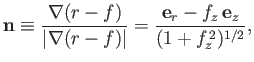
![$\displaystyle \nabla\cdot {\bf n} = \frac{1}{f\,f_z}\,\frac{d}{dz}\!\left[\frac{f}{(1+f_z^{\,2})^{1/2}}\right].$](img1235.png)
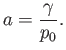
![]() , where
, where ![]() , and has a fixed
radius at its two end-points,
, and has a fixed
radius at its two end-points, ![]() and
and ![]() .
This could most easily be achieved by supporting the
bubble on two rigid parallel co-axial rings located at
.
This could most easily be achieved by supporting the
bubble on two rigid parallel co-axial rings located at ![]() and
and ![]() .
The net free energy required to create the bubble can be written
.
The net free energy required to create the bubble can be written
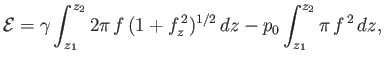
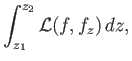
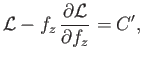
![$\displaystyle 2\pi\,\gamma\left[\frac{f}{(1+f_z^{\,2})^{1/2}}-\frac{f^{\,2}}{2\,a}\right] = C',$](img1252.png)
![]() , in which there is no pressure difference across the surface of the bubble.
In this situation, writing
, in which there is no pressure difference across the surface of the bubble.
In this situation, writing
![]() , Equation (3.59) reduces to
, Equation (3.59) reduces to

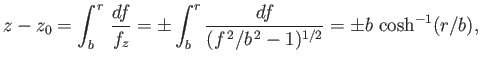

![]() that are located a perpendicular
distance
that are located a perpendicular
distance ![]() apart. Without loss of generality, we can specify that the rings lie at
apart. Without loss of generality, we can specify that the rings lie at ![]() . It follows,
from Equation (3.69), that
. It follows,
from Equation (3.69), that ![]() , and
, and
![]() and
and ![]() , in which case the previous equation becomes
, in which case the previous equation becomes
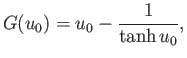
![]() , in which there is a pressure difference across the surface of the bubble.
In this situation, writing
, in which there is a pressure difference across the surface of the bubble.
In this situation, writing
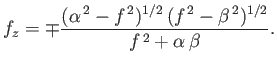
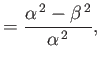
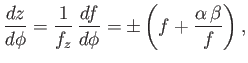
![]() and
and ![]() . It follows that
. It follows that
![]() for
for
![]() , and
, and
![]() for
for
![]() , where
, where
![]() and
and ![]() . It follows that
. It follows that
![]() for
for
![]() , and
, and
![]() for
for
![]() , where
, where
![]() , and
, and
![]() and
and ![]() . It follows that
. It follows that
![]() for
for
![]() (or
(or
![]() ), and
), and
![]() for
for
![]() , where
, where