


Next: Spherical Interfaces
Up: Surface Tension
Previous: Introduction
Young-Laplace Equation
Consider an interface separating two immiscible fluids that are in equilibrium with one another. Let these two
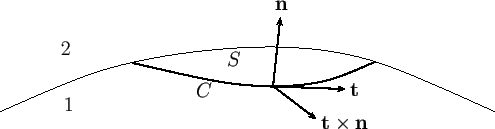
fluids be denoted 1 and 2. Consider an arbitrary segment 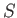 of this interface that is enclosed by some closed curve
of this interface that is enclosed by some closed curve 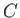 .
Let
.
Let 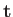 denote a unit tangent to the curve, and let
denote a unit tangent to the curve, and let 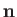 denote a unit normal to the
interface directed from fluid 1 to fluid 2. (Note that
denote a unit normal to the
interface directed from fluid 1 to fluid 2. (Note that 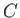 circulates around
circulates around 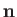 in a
right-handed manner. See Figure 3.1.) Suppose that
in a
right-handed manner. See Figure 3.1.) Suppose that 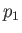 and
and 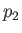 are the
pressures of fluids 1 and 2, respectively, on either side of
are the
pressures of fluids 1 and 2, respectively, on either side of 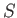 . Finally, let
. Finally, let 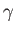 be the (uniform)
surface tension at the interface.
be the (uniform)
surface tension at the interface.
Figure 3.1:
Interface between two immiscible fluids.
 |
The net force acting on 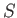 is
is
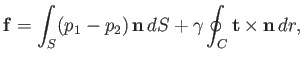 |
(3.1) |
where
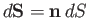 is an element of
is an element of 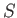 , and
, and
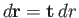 an element of
an element of 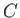 . Here, the first term on the
right-hand side is the net normal force due to the pressure difference across the interface, whereas the
second term is the net surface tension force.
Note that body forces play no role in Equation (3.1), because the interface has zero volume. Furthermore,
viscous forces can be neglected, because both fluids are static.
In equilibrium,
the net force acting on
. Here, the first term on the
right-hand side is the net normal force due to the pressure difference across the interface, whereas the
second term is the net surface tension force.
Note that body forces play no role in Equation (3.1), because the interface has zero volume. Furthermore,
viscous forces can be neglected, because both fluids are static.
In equilibrium,
the net force acting on 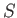 must be zero: that is,
must be zero: that is,
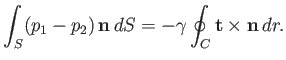 |
(3.2) |
(In fact, the net force would be zero even in the absence of equilibrium, because the interface has zero mass.)
Applying the curl theorem (see Section A.22) to the curve 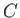 , we find that
, we find that
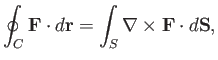 |
(3.3) |
where 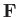 is a general vector field. This theorem can also be written
is a general vector field. This theorem can also be written
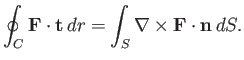 |
(3.4) |
Suppose that
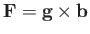 , where
, where 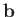 is an arbitrary constant vector. We obtain
is an arbitrary constant vector. We obtain
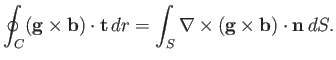 |
(3.5) |
However, the vector identity (A.179) yields
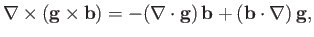 |
(3.6) |
as 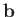 is a constant vector.
Hence, we get
is a constant vector.
Hence, we get
![$\displaystyle {\bf b}\cdot\oint_C {\bf t}\times {\bf g}\,dr = {\bf b}\cdot\!\int_S[(\nabla {\bf g})\cdot{\bf n} - (\nabla\cdot{\bf g})\,{\bf n}]\,dS,$](img1099.png) |
(3.7) |
where
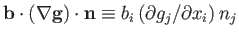 .
Now, because
.
Now, because 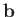 is also an arbitrary vector, the previous equation gives
is also an arbitrary vector, the previous equation gives
![$\displaystyle \oint_C {\bf t}\times {\bf g}\,dr = \int_S\left[(\nabla {\bf g})\cdot{\bf n} - (\nabla\cdot{\bf g})\,{\bf n}\right]dS.$](img1101.png) |
(3.8) |
Taking
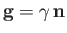 , we find that
, we find that
![$\displaystyle \gamma\oint_C {\bf t}\times {\bf n}\,dr= \gamma\int_S \left[(\nabla {\bf n})\cdot {\bf n} - (\nabla\cdot {\bf n})\,{\bf n}\right]dS.$](img1103.png) |
(3.9) |
But,
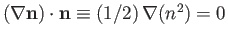 , because
, because 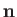 is a unit vector. Thus, we obtain
is a unit vector. Thus, we obtain
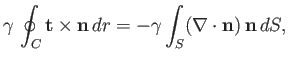 |
(3.10) |
which can be combined with Equation (3.2) to give
![$\displaystyle \int_S\left[(p_1-p_2)-\gamma\,(\nabla\cdot{\bf n})\right]{\bf n}\,dS = 0.$](img1106.png) |
(3.11) |
Finally, given that 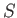 is arbitrary, the previous expression reduces to the pressure balance constraint
is arbitrary, the previous expression reduces to the pressure balance constraint
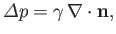 |
(3.12) |
where
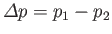 .
The previous relation is generally known as the Young-Laplace equation, and is named after Thomas Young (1773-1829), who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace (1749-1827) who completed the mathematical description in the following year.
The Young-Laplace equation
can also be derived by minimizing the free energy of the interface. (See Section 3.8.) Note that
.
The previous relation is generally known as the Young-Laplace equation, and is named after Thomas Young (1773-1829), who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace (1749-1827) who completed the mathematical description in the following year.
The Young-Laplace equation
can also be derived by minimizing the free energy of the interface. (See Section 3.8.) Note that
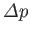 is
the jump in pressure seen when crossing the interface in the opposite direction to
is
the jump in pressure seen when crossing the interface in the opposite direction to 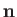 .
Of course, a plane interface is characterized by
.
Of course, a plane interface is characterized by
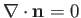 . On the other hand, a curved
interface generally has
. On the other hand, a curved
interface generally has
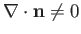 . In fact,
. In fact,
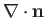 measures the local
mean curvature of the interface. Thus, according to the Young-Laplace equation, there is a pressure jump across
a curved interface between two immiscible fluids, the
magnitude of the jump being proportional to the surface tension.
measures the local
mean curvature of the interface. Thus, according to the Young-Laplace equation, there is a pressure jump across
a curved interface between two immiscible fluids, the
magnitude of the jump being proportional to the surface tension.



Next: Spherical Interfaces
Up: Surface Tension
Previous: Introduction
Richard Fitzpatrick
2016-01-22

![]() is
is
![]() , we find that
, we find that
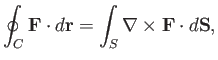
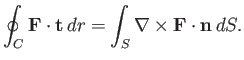
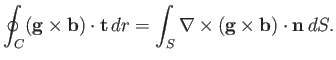
![$\displaystyle {\bf b}\cdot\oint_C {\bf t}\times {\bf g}\,dr = {\bf b}\cdot\!\int_S[(\nabla {\bf g})\cdot{\bf n} - (\nabla\cdot{\bf g})\,{\bf n}]\,dS,$](img1099.png)
![$\displaystyle \oint_C {\bf t}\times {\bf g}\,dr = \int_S\left[(\nabla {\bf g})\cdot{\bf n} - (\nabla\cdot{\bf g})\,{\bf n}\right]dS.$](img1101.png)
![$\displaystyle \gamma\oint_C {\bf t}\times {\bf n}\,dr= \gamma\int_S \left[(\nabla {\bf n})\cdot {\bf n} - (\nabla\cdot {\bf n})\,{\bf n}\right]dS.$](img1103.png)
![$\displaystyle \int_S\left[(p_1-p_2)-\gamma\,(\nabla\cdot{\bf n})\right]{\bf n}\,dS = 0.$](img1106.png)