


Next: Useful Vector Identities
Up: Vectors and Vector Fields
Previous: Laplacian Operator
Curl
Consider a vector field
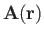 , and a loop that lies in one plane.
The integral of
, and a loop that lies in one plane.
The integral of 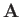 around this loop is written
around this loop is written
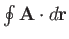 , where
, where 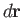 is a line element of the
loop. If
is a line element of the
loop. If 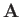 is a conservative field then
is a conservative field then
 and
and
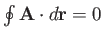 for all loops. In general, for a non-conservative field,
for all loops. In general, for a non-conservative field,
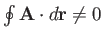 .
.
For a small loop, we expect
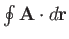 to be proportional to
the area of the loop. Moreover, for a fixed-area loop, we expect
to be proportional to
the area of the loop. Moreover, for a fixed-area loop, we expect
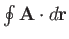 to depend on the orientation of the loop.
One particular orientation will give the maximum value:
to depend on the orientation of the loop.
One particular orientation will give the maximum value:
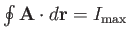 . If the loop subtends an angle
. If the loop subtends an angle 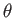 with this optimum orientation
then we expect
with this optimum orientation
then we expect
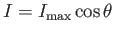 . Let us introduce the vector field
. Let us introduce the vector field
 whose magnitude is
whose magnitude is
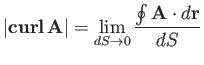 |
(A.150) |
for the orientation giving
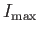 . Here,
. Here, 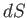 is the area of the loop.
The direction of
is the area of the loop.
The direction of
 is perpendicular to the plane of the loop,
when it is
in the
orientation giving
is perpendicular to the plane of the loop,
when it is
in the
orientation giving
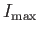 , with the sense given by a right-hand circulation rule.
, with the sense given by a right-hand circulation rule.
Let us now express
 in terms of the components of
in terms of the components of 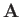 .
First, we shall
evaluate
.
First, we shall
evaluate
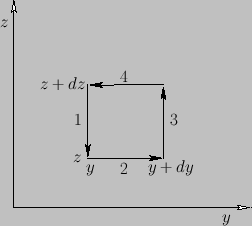
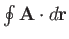 around a small rectangle in the
around a small rectangle in the
 -
- plane, as shown in Figure A.25.
The contribution from sides 1 and 3 is
plane, as shown in Figure A.25.
The contribution from sides 1 and 3 is
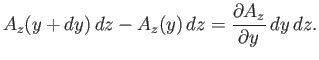 |
(A.151) |
The contribution from sides 2 and 4 is
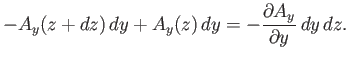 |
(A.152) |
So, the total of all contributions gives
 |
(A.153) |
where 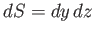 is the area of the loop.
is the area of the loop.
Figure:
A vector line integral around a small rectangular loop in the  -
- plane.
plane.
 |
Consider a non-rectangular (but still small) loop in the  -
- plane.
We can divide it into rectangular
elements, and form
plane.
We can divide it into rectangular
elements, and form
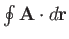 over all the resultant
loops. The interior
contributions cancel, so we are just left with the contribution from the outer loop.
Also, the area of the outer loop is the sum of all the areas of the inner loops.
We conclude that
over all the resultant
loops. The interior
contributions cancel, so we are just left with the contribution from the outer loop.
Also, the area of the outer loop is the sum of all the areas of the inner loops.
We conclude that
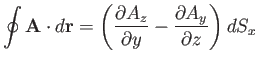 |
(A.154) |
is valid for a small loop
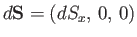 of any shape in the
of any shape in the  -
- plane. Likewise, we can show that
if the loop is in the
plane. Likewise, we can show that
if the loop is in the  -
- plane then
plane then
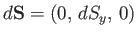 and
and
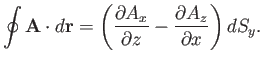 |
(A.155) |
Finally, if the loop is in the  -
- plane then
plane then
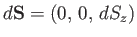 and
and
 |
(A.156) |
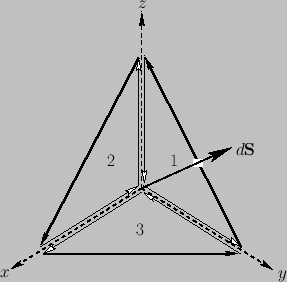
Imagine an arbitrary loop of vector area
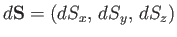 . We
can construct this out of three vector areas,
. We
can construct this out of three vector areas,  ,
,  , and
, and 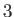 , directed in the
, directed in the  -,
-,  -, and
-, and  -directions, respectively, as
indicated in Figure A.26.
If we form the line integral around all three loops then the interior contributions
cancel, and we are left with the line integral around the original loop. Thus,
-directions, respectively, as
indicated in Figure A.26.
If we form the line integral around all three loops then the interior contributions
cancel, and we are left with the line integral around the original loop. Thus,
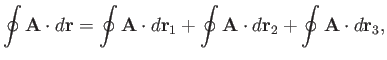 |
(A.157) |
giving
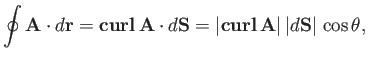 |
(A.158) |
where
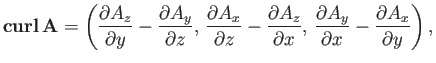 |
(A.159) |
and 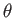 is the angle subtended between the directions of
is the angle subtended between the directions of
 and
and 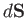 .
Note that
.
Note that
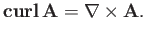 |
(A.160) |
This demonstrates that
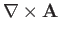 is a good vector field, because it is
the cross product of the
is a good vector field, because it is
the cross product of the  operator (a good vector operator) and
the vector field
operator (a good vector operator) and
the vector field 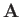 .
.
Figure A.26:
Decomposition of a vector area into its Cartesian components.
 |
Consider a solid body rotating about the  -axis. The angular velocity is given
by
-axis. The angular velocity is given
by
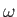
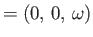 , so the rotation velocity at
position
, so the rotation velocity at
position  is
is
[See Equation (A.52).]
Let us evaluate
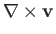 on the axis of
rotation. The
on the axis of
rotation. The  -component is proportional to the
integral
-component is proportional to the
integral
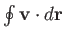 around a loop in the
around a loop in the  -
- plane. This is
plainly zero. Likewise, the
plane. This is
plainly zero. Likewise, the  -component is also zero. The
-component is also zero. The  -component
is
-component
is
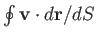 around some loop in the
around some loop in the  -
- plane.
Consider a circular loop. We have
plane.
Consider a circular loop. We have
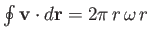 with
with
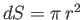 .
Here,
.
Here, 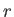 is the perpendicular distance from the rotation axis.
It follows that
is the perpendicular distance from the rotation axis.
It follows that
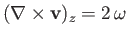 , which
is independent of
, which
is independent of 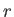 . So, on the axis,
. So, on the axis,
 .
Off the axis, at position
.
Off the axis, at position  , we can write
, we can write
The first part has the same curl as the velocity field on the axis, and the
second part has zero curl, because it is constant. Thus,
 everywhere in the body. This allows us to
form a physical picture of
everywhere in the body. This allows us to
form a physical picture of
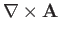 . If we imagine
. If we imagine
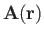 as the
velocity field of some fluid then
as the
velocity field of some fluid then
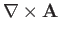 at any given point is equal
to twice the local angular rotation velocity:
that is, 2
at any given point is equal
to twice the local angular rotation velocity:
that is, 2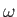 .
Hence, a vector field with
.
Hence, a vector field with
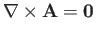 everywhere is said to
be irrotational.
everywhere is said to
be irrotational.
Another important result of vector field theory is the curl theorem:
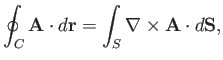 |
(A.163) |
for some (non-planar) surface  bounded by a rim
bounded by a rim 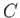 . This theorem can easily
be proved by splitting the loop up into many small rectangular loops, and forming
the integral around all of the resultant loops. All of the contributions from the
interior loops cancel, leaving just the contribution from the outer rim.
Making use of Equation (A.158) for each of the small loops, we can see that the contribution
from all of the loops is also equal to the integral of
. This theorem can easily
be proved by splitting the loop up into many small rectangular loops, and forming
the integral around all of the resultant loops. All of the contributions from the
interior loops cancel, leaving just the contribution from the outer rim.
Making use of Equation (A.158) for each of the small loops, we can see that the contribution
from all of the loops is also equal to the integral of
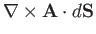 across the whole surface. This proves the theorem.
across the whole surface. This proves the theorem.
One immediate consequence of the curl theorem is that
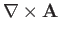 is ``incompressible.'' Consider any two surfaces,
is ``incompressible.'' Consider any two surfaces, 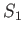 and
and 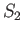 , that share the
same rim. (See Figure A.23.) It is clear from the curl theorem that
, that share the
same rim. (See Figure A.23.) It is clear from the curl theorem that
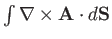 is the same for both surfaces. Thus, it
follows that
is the same for both surfaces. Thus, it
follows that
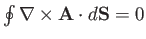 for any closed surface.
However, we have from the divergence theorem that
for any closed surface.
However, we have from the divergence theorem that
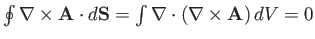 for any volume. Hence,
for any volume. Hence,
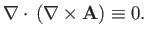 |
(A.164) |
So,
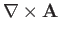 is a solenoidal field.
is a solenoidal field.
We have seen that for a conservative field
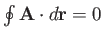 for any loop. This is entirely equivalent to
for any loop. This is entirely equivalent to
 .
However, the magnitude of
.
However, the magnitude of
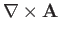 is
is
 for some
particular loop. It is clear then that
for some
particular loop. It is clear then that
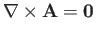 for a conservative field. In other words,
for a conservative field. In other words,
 |
(A.165) |
Thus, a conservative field is also an irrotational one.



Next: Useful Vector Identities
Up: Vectors and Vector Fields
Previous: Laplacian Operator
Richard Fitzpatrick
2016-01-22
![]() to be proportional to
the area of the loop. Moreover, for a fixed-area loop, we expect
to be proportional to
the area of the loop. Moreover, for a fixed-area loop, we expect
![]() to depend on the orientation of the loop.
One particular orientation will give the maximum value:
to depend on the orientation of the loop.
One particular orientation will give the maximum value:
![]() . If the loop subtends an angle
. If the loop subtends an angle ![]() with this optimum orientation
then we expect
with this optimum orientation
then we expect
![]() . Let us introduce the vector field
. Let us introduce the vector field
![]() whose magnitude is
whose magnitude is
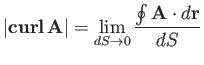
![]() in terms of the components of
in terms of the components of ![]() .
First, we shall
evaluate
.
First, we shall
evaluate
![]() around a small rectangle in the
around a small rectangle in the
![]() -
-![]() plane, as shown in Figure A.25.
The contribution from sides 1 and 3 is
plane, as shown in Figure A.25.
The contribution from sides 1 and 3 is
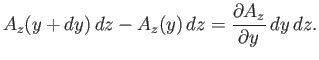
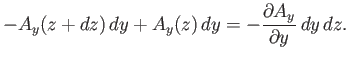

![]() -
-![]() plane.
We can divide it into rectangular
elements, and form
plane.
We can divide it into rectangular
elements, and form
![]() over all the resultant
loops. The interior
contributions cancel, so we are just left with the contribution from the outer loop.
Also, the area of the outer loop is the sum of all the areas of the inner loops.
We conclude that
over all the resultant
loops. The interior
contributions cancel, so we are just left with the contribution from the outer loop.
Also, the area of the outer loop is the sum of all the areas of the inner loops.
We conclude that
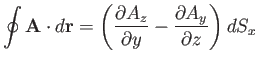
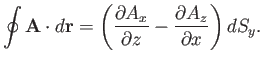

![]() . We
can construct this out of three vector areas,
. We
can construct this out of three vector areas, ![]() ,
, ![]() , and
, and ![]() , directed in the
, directed in the ![]() -,
-, ![]() -, and
-, and ![]() -directions, respectively, as
indicated in Figure A.26.
If we form the line integral around all three loops then the interior contributions
cancel, and we are left with the line integral around the original loop. Thus,
-directions, respectively, as
indicated in Figure A.26.
If we form the line integral around all three loops then the interior contributions
cancel, and we are left with the line integral around the original loop. Thus,
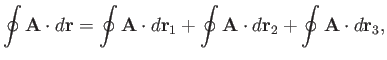
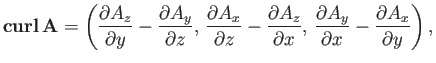
![]() -axis. The angular velocity is given
by
-axis. The angular velocity is given
by
![]()
![]() , so the rotation velocity at
position
, so the rotation velocity at
position ![]() is
is
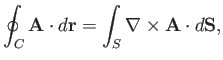
![]() is ``incompressible.'' Consider any two surfaces,
is ``incompressible.'' Consider any two surfaces, ![]() and
and ![]() , that share the
same rim. (See Figure A.23.) It is clear from the curl theorem that
, that share the
same rim. (See Figure A.23.) It is clear from the curl theorem that
![]() is the same for both surfaces. Thus, it
follows that
is the same for both surfaces. Thus, it
follows that
![]() for any closed surface.
However, we have from the divergence theorem that
for any closed surface.
However, we have from the divergence theorem that
![]() for any volume. Hence,
for any volume. Hence,
![]() for any loop. This is entirely equivalent to
for any loop. This is entirely equivalent to
![]() .
However, the magnitude of
.
However, the magnitude of
![]() is
is
![]() for some
particular loop. It is clear then that
for some
particular loop. It is clear then that
![]() for a conservative field. In other words,
for a conservative field. In other words,