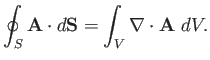Next: Laplacian Operator
Up: Vectors and Vector Fields
Previous: Grad Operator
Divergence
Let us start with a vector field
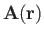 . Consider
. Consider
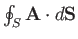 over some closed surface
over some closed surface  , where
, where 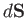 denotes an outward
pointing surface element. This surface integral is usually called the
flux of
denotes an outward
pointing surface element. This surface integral is usually called the
flux of 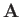 out of
out of  . If
. If 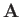 represents the velocity of some fluid
then
represents the velocity of some fluid
then
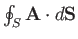 is the rate of fluid flow out of
is the rate of fluid flow out of  .
.
If 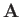 is constant in space then it is easily demonstrated that the net
flux out of
is constant in space then it is easily demonstrated that the net
flux out of  is zero. In fact,
is zero. In fact,
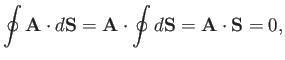 |
(A.129) |
because the vector area  of a closed surface is zero.
of a closed surface is zero.
Figure A.21:
Flux of a vector field out of a small box.
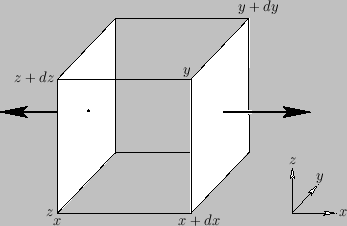 |
Suppose, now, that 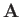 is not uniform in space. Consider a very small
rectangular volume over which
is not uniform in space. Consider a very small
rectangular volume over which 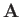 hardly varies. The contribution to
hardly varies. The contribution to
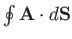 from the two faces normal to the
from the two faces normal to the  -axis is
-axis is
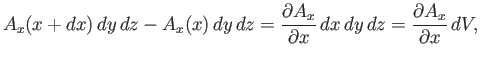 |
(A.130) |
where
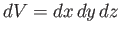 is the volume element. (See Figure A.21.)
There are analogous contributions
from the sides normal to the
is the volume element. (See Figure A.21.)
There are analogous contributions
from the sides normal to the  - and
- and  -axes, so the total of all the contributions
is
-axes, so the total of all the contributions
is
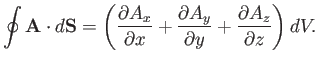 |
(A.131) |
The divergence of a vector field is defined
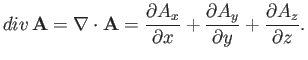 |
(A.132) |
Divergence is a good scalar (i.e., it is coordinate
independent),
because it is the dot product of
the vector operator  with
with 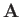 . The formal definition of
. The formal definition of
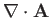 is
is
 |
(A.133) |
This definition is independent of the shape of the infinitesimal volume
element.
One of the most important results in vector field theory is the so-called
divergence theorem. This states that for any volume
 surrounded by a closed surface
surrounded by a closed surface  ,
,
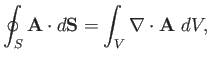 |
(A.134) |
where 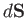 is an outward pointing volume element.
The proof is very
straightforward. We divide up the volume into very many infinitesimal cubes, and
sum
is an outward pointing volume element.
The proof is very
straightforward. We divide up the volume into very many infinitesimal cubes, and
sum
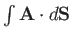 over all of the surfaces. The contributions
from the interior surfaces cancel out, leaving just the contribution from the outer
surface. (See Figure A.22.) We can use Equation (A.131) for each cube individually. This tells us that
the summation is equivalent to
over all of the surfaces. The contributions
from the interior surfaces cancel out, leaving just the contribution from the outer
surface. (See Figure A.22.) We can use Equation (A.131) for each cube individually. This tells us that
the summation is equivalent to
 over the whole
volume. Thus, the integral of
over the whole
volume. Thus, the integral of
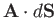 over the outer surface is
equal to the integral of
over the outer surface is
equal to the integral of
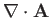 over the whole volume, which
proves the divergence theorem.
over the whole volume, which
proves the divergence theorem.
Figure A.22:
The divergence theorem.
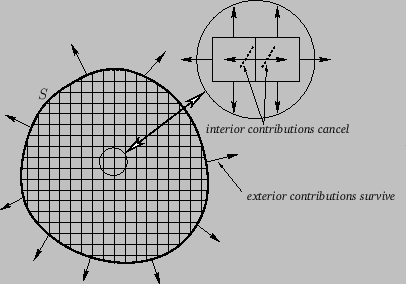 |
Now, for a vector field with
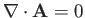 ,
,
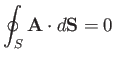 |
(A.135) |
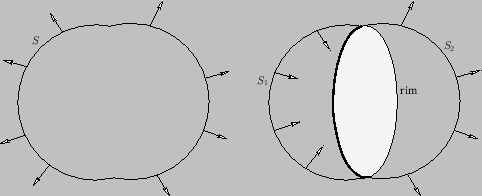
for any closed surface  . So, for two surfaces,
. So, for two surfaces,
 and
and 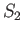 , on the same rim,
, on the same rim,
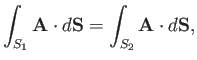 |
(A.136) |
as illustrated in Figure A.23. (Note that the direction of the surface elements on 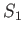 has been reversed relative to those on the closed surface. Hence, the
sign of the associated surface integral is also reversed.)
Thus, if
has been reversed relative to those on the closed surface. Hence, the
sign of the associated surface integral is also reversed.)
Thus, if
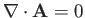 then the surface integral depends on the rim, but
not on the nature of the surface that spans it.
On the other hand, if
then the surface integral depends on the rim, but
not on the nature of the surface that spans it.
On the other hand, if
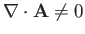 then the integral
depends on both the rim and the surface.
then the integral
depends on both the rim and the surface.
Figure A.23:
Two surfaces spanning the same rim (right), and the
equivalent closed surface (left).
 |
Consider an incompressible fluid whose velocity field is  . It is clear that
. It is clear that
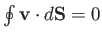 for any closed surface, because what flows into the
surface must flow out again. Thus, according to the divergence theorem,
for any closed surface, because what flows into the
surface must flow out again. Thus, according to the divergence theorem,
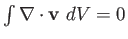 for any volume. The only way in which this is
possible is if
for any volume. The only way in which this is
possible is if
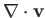 is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
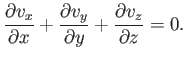 |
(A.137) |
It is sometimes helpful to represent a vector field  by lines of force
or field-lines.
The direction of a line of force at any point is the same as the local direction of
by lines of force
or field-lines.
The direction of a line of force at any point is the same as the local direction of
 . The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to
. The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to 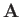 ) is equal to
) is equal to  .
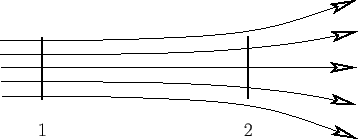
For instance, in Figure A.24,
.
For instance, in Figure A.24,  is larger at point 1 than at point 2. The number of lines
crossing a surface element
is larger at point 1 than at point 2. The number of lines
crossing a surface element 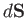 is
is
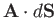 . So, the
net number of lines leaving a closed surface is
. So, the
net number of lines leaving a closed surface is
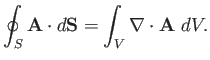 |
(A.138) |
If
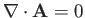 then there is no net flux of lines out of any surface.
Such a field is
called a solenoidal vector field. The simplest example of a solenoidal vector
field is one in which the lines of force all form closed loops.
then there is no net flux of lines out of any surface.
Such a field is
called a solenoidal vector field. The simplest example of a solenoidal vector
field is one in which the lines of force all form closed loops.
Figure A.24:
Divergent lines of force.
 |



Next: Laplacian Operator
Up: Vectors and Vector Fields
Previous: Grad Operator
Richard Fitzpatrick
2016-01-22
![]() is constant in space then it is easily demonstrated that the net
flux out of
is constant in space then it is easily demonstrated that the net
flux out of ![]() is zero. In fact,
is zero. In fact,
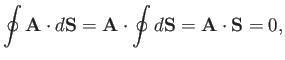
![]() is not uniform in space. Consider a very small
rectangular volume over which
is not uniform in space. Consider a very small
rectangular volume over which ![]() hardly varies. The contribution to
hardly varies. The contribution to
![]() from the two faces normal to the
from the two faces normal to the ![]() -axis is
-axis is
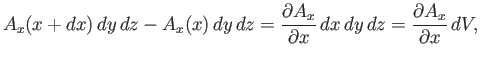
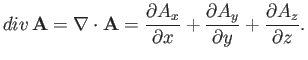

![]() surrounded by a closed surface
surrounded by a closed surface ![]() ,
,
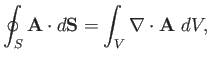
![]() ,
,
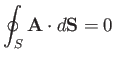
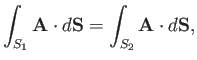
![]() . It is clear that
. It is clear that
![]() for any closed surface, because what flows into the
surface must flow out again. Thus, according to the divergence theorem,
for any closed surface, because what flows into the
surface must flow out again. Thus, according to the divergence theorem,
![]() for any volume. The only way in which this is
possible is if
for any volume. The only way in which this is
possible is if
![]() is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
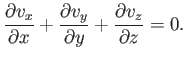
![]() by lines of force
or field-lines.
The direction of a line of force at any point is the same as the local direction of
by lines of force
or field-lines.
The direction of a line of force at any point is the same as the local direction of
![]() . The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to
. The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to ![]() ) is equal to
) is equal to ![]() .
For instance, in Figure A.24,
.
For instance, in Figure A.24, ![]() is larger at point 1 than at point 2. The number of lines
crossing a surface element
is larger at point 1 than at point 2. The number of lines
crossing a surface element ![]() is
is
![]() . So, the
net number of lines leaving a closed surface is
. So, the
net number of lines leaving a closed surface is