


Next: Equilibrium of Floating Bodies
Up: Hydrostatics
Previous: Hydrostatic Pressure
Buoyancy
Consider the air/water system described in the previous section.
Let  be some volume, bounded by a closed surface
be some volume, bounded by a closed surface  , that straddles the plane
, that straddles the plane  , and is thus partially occupied by water, and partially
by air. The
, and is thus partially occupied by water, and partially
by air. The 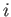 -component of the net force acting on the fluid (i.e., either water or air) contained within
-component of the net force acting on the fluid (i.e., either water or air) contained within  is written (see Section 1.3)
is written (see Section 1.3)
 |
(2.5) |
where
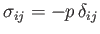 |
(2.6) |
is the stress tensor for a static fluid (see Section 1.5), and
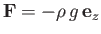 |
(2.7) |
the gravitational force density. (Recall that the indices  ,
,  , and
, and 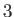 refer to the
refer to the  -,
-,  -, and
-, and  -axes, respectively. Thus,
-axes, respectively. Thus,
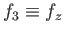 , et cetera.)
The first term on the right-hand side of Equation (2.5) represents the net surface force acting across
, et cetera.)
The first term on the right-hand side of Equation (2.5) represents the net surface force acting across
 , whereas the second term represents the net volume force distributed throughout
, whereas the second term represents the net volume force distributed throughout  .
Making use of the tensor divergence theorem (see Section B.4), Equations (2.5)-(2.7)
yield the following expression for the net force:
.
Making use of the tensor divergence theorem (see Section B.4), Equations (2.5)-(2.7)
yield the following expression for the net force:
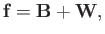 |
(2.8) |
where
 |
(2.9) |
and
Here, 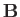 is the net surface force, and
is the net surface force, and  the net volume force.
the net volume force.
It follows from Equations (2.4) and (2.9) that
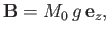 |
(2.12) |
where
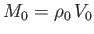 .
Here,
.
Here, 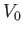 is the volume of that part of
is the volume of that part of  which lies below the waterline, and
which lies below the waterline, and 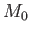 the
total mass of water contained within
the
total mass of water contained within  .
Moreover, from Equations (2.2), (2.10), and (2.11),
.
Moreover, from Equations (2.2), (2.10), and (2.11),
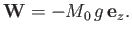 |
(2.13) |
It can be seen that the net surface force, 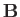 , is directed vertically upward, and exactly balances the
net volume force,
, is directed vertically upward, and exactly balances the
net volume force,  , which is directed vertically downward. Of course,
, which is directed vertically downward. Of course,  is the weight of the water contained
within
is the weight of the water contained
within  . On the other hand,
. On the other hand, 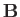 , which is generally known as the buoyancy force,
is the resultant pressure of the water immediately surrounding
, which is generally known as the buoyancy force,
is the resultant pressure of the water immediately surrounding  . We conclude that, in equilibrium, the net buoyancy force acting across
. We conclude that, in equilibrium, the net buoyancy force acting across  exactly balances the weight of the water inside
exactly balances the weight of the water inside  , so that the total force acting on the contents of
, so that the total force acting on the contents of  is zero, as
must be the case for a system in mechanical equilibrium. We can also deduce that
the line of action of
is zero, as
must be the case for a system in mechanical equilibrium. We can also deduce that
the line of action of 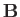 (which is vertical) passes through the center of gravity of the water inside
(which is vertical) passes through the center of gravity of the water inside  . Otherwise, a net torque would act on the contents of
. Otherwise, a net torque would act on the contents of  , which would contradict our assumption that the system is in
mechanical equilibrium.
, which would contradict our assumption that the system is in
mechanical equilibrium.



Next: Equilibrium of Floating Bodies
Up: Hydrostatics
Previous: Hydrostatic Pressure
Richard Fitzpatrick
2016-01-22
