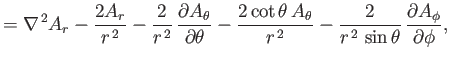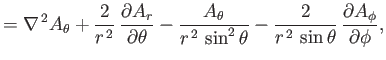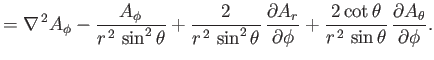Next: Exercises
Up: Non-Cartesian Coordinates
Previous: Cylindrical Coordinates
Spherical Coordinates
In the spherical coordinate system,  ,
,
 , and
, and 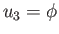 ,
where
,
where
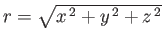 ,
,
 ,
,
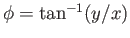 , and
, and  ,
,  ,
,  are standard Cartesian coordinates.
Thus,
are standard Cartesian coordinates.
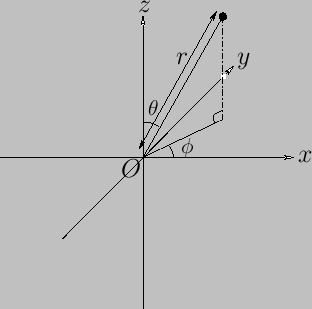
Thus, 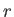 is the length of the radius vector,
is the length of the radius vector, 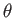 the angle subtended between the radius vector and the
the angle subtended between the radius vector and the  -axis, and
-axis, and 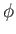 the angle subtended between the projection of the radius vector
onto the
the angle subtended between the projection of the radius vector
onto the  -
- plane and the
plane and the  -axis. (See Figure C.2.)
-axis. (See Figure C.2.)
Figure C.2:
Spherical coordinates.
 |
A general vector 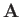 is written
is written
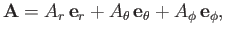 |
(C.55) |
where
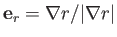 ,
,
 , and
, and
 . Of course, the unit vectors
. Of course, the unit vectors
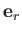 ,
,
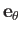 , and
, and
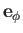 are mutually orthogonal, so
are mutually orthogonal, so
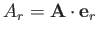 , et cetera.
, et cetera.
As is easily demonstrated, an element of length (squared) in the spherical coordinate system takes the form
 |
(C.56) |
Hence, comparison with Equation (C.6) reveals that the scale factors for this system are
Thus, surface elements normal to 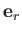 ,
,
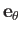 , and
, and
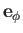 are
written
are
written
respectively, whereas
a
volume element takes the form
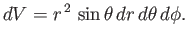 |
(C.63) |
According to Equations (C.13), (C.15), and (C.18), gradient, divergence, and curl in the spherical
coordinate system are written
respectively. Here,
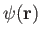 is a general scalar field, and
is a general scalar field, and
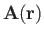 a general vector field.
a general vector field.
According to Equation (C.19), when expressed in spherical coordinates, the Laplacian of a scalar field becomes
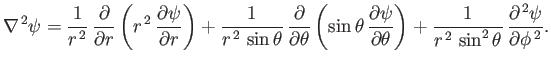 |
(C.67) |
Moreover, from Equation (C.23), the components of
 in the spherical coordinate system are
in the spherical coordinate system are
Now, according to Equation (C.26), the components of
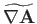 in the spherical
coordinate system are
in the spherical
coordinate system are
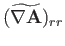 |
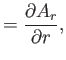 |
(C.71) |
 |
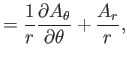 |
(C.72) |
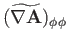 |
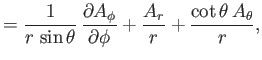 |
(C.73) |
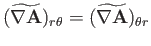 |
 |
(C.74) |
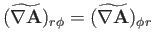 |
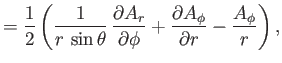 |
(C.75) |
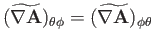 |
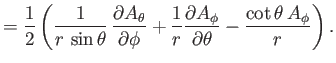 |
(C.76) |
Finally, from Equation (C.28), the components of
 in the
spherical coordinate system are
in the
spherical coordinate system are



Next: Exercises
Up: Non-Cartesian Coordinates
Previous: Cylindrical Coordinates
Richard Fitzpatrick
2016-01-22

![]() is written
is written
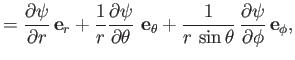

![$\displaystyle = \left[\frac{1}{r\,\sin\theta}\,\frac{\partial}{\partial \theta}...
...frac{1}{r\,\sin\theta}\,\frac{\partial A_\theta}{\partial \phi}\right]{\bf e}_r$](img7177.png)
![$\displaystyle \phantom{=}+\left[\frac{1}{r\,\sin\theta}\,\frac{\partial A_r}{\p...
... \phi}-\frac{1}{r}\frac{\partial}{\partial r}\,(r\,A_\phi)\right]{\bf e}_\theta$](img7178.png)
![$\displaystyle \phantom{=}+ \left[\frac{1}{r}\,\frac{\partial}{\partial r}\,(r\,A_\theta) - \frac{1}{r}\,\frac{\partial A_r}{\partial\theta}\right]{\bf e}_\phi,\ $](img7179.png)
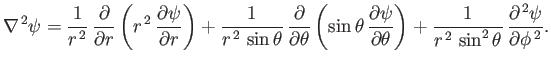
![]() in the spherical coordinate system are
in the spherical coordinate system are

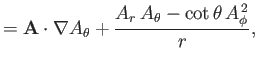
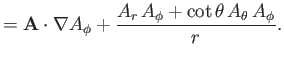
![]() in the spherical
coordinate system are
in the spherical
coordinate system are
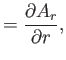
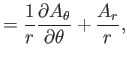
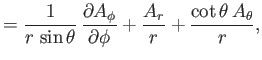

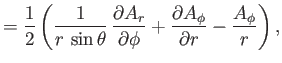
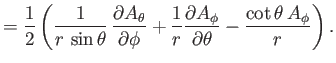
![]() in the
spherical coordinate system are
in the
spherical coordinate system are