


Next: Cylindrical Coordinates
Up: Non-Cartesian Coordinates
Previous: Introduction
Let 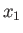 ,
, 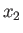 ,
, 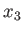 be a set of standard right-handed Cartesian coordinates. Furthermore, let
be a set of standard right-handed Cartesian coordinates. Furthermore, let
 ,
,
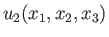 ,
,
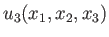 be three independent functions of these coordinates which are
such that each unique triplet of
be three independent functions of these coordinates which are
such that each unique triplet of 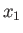 ,
, 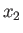 ,
, 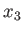 values is associated with a unique triplet of
values is associated with a unique triplet of
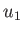 ,
, 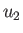 ,
, 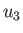 values. It follows that
values. It follows that 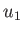 ,
, 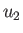 ,
, 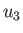 can be used as an alternative set of coordinates to
distinguish different points in space. Because the surfaces of constant
can be used as an alternative set of coordinates to
distinguish different points in space. Because the surfaces of constant 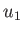 ,
, 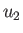 , and
, and 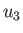 are not
generally parallel planes, but rather curved surfaces, this type of coordinate system is termed curvilinear.
are not
generally parallel planes, but rather curved surfaces, this type of coordinate system is termed curvilinear.
Let
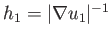 ,
,
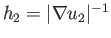 , and
, and
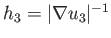 . It follows that
. It follows that
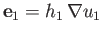 ,
,
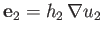 , and
, and
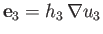 are
a set of unit basis vectors that are normal to surfaces of constant
are
a set of unit basis vectors that are normal to surfaces of constant 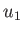 ,
, 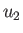 , and
, and 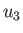 , respectively, at all points
in space. Note, however, that the direction of these basis vectors is generally a function of position. Suppose that
the
, respectively, at all points
in space. Note, however, that the direction of these basis vectors is generally a function of position. Suppose that
the 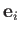 , where
, where 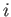 runs from 1 to 3, are mutually orthogonal at all points in space: that is,
runs from 1 to 3, are mutually orthogonal at all points in space: that is,
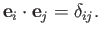 |
(C.1) |
In this case, 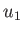 ,
, 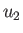 ,
, 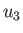 are said to constitute an orthogonal coordinate system.
Suppose, further, that
are said to constitute an orthogonal coordinate system.
Suppose, further, that
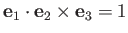 |
(C.2) |
at all points in space, so that 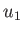 ,
, 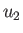 ,
, 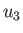 also constitute a right-handed
coordinate system. It follows that
also constitute a right-handed
coordinate system. It follows that
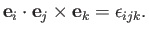 |
(C.3) |
Finally, a general vector 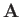 , associated with a particular point in space, can be written
, associated with a particular point in space, can be written
 |
(C.4) |
where the 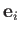 are the local basis vectors of the
are the local basis vectors of the 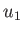 ,
, 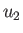 ,
, 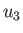 system, and
system, and
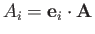 is termed the
is termed the 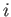 th component of
th component of 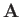 in this system.
in this system.
Consider two neighboring points in space whose coordinates in the 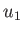 ,
, 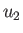 ,
, 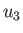 system are
system are 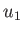 ,
, 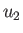 ,
, 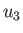 and
and 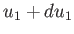 ,
, 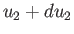 ,
,  .
It is easily shown that the vector directed from the first to the second of these points takes the form
.
It is easily shown that the vector directed from the first to the second of these points takes the form
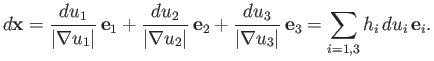 |
(C.5) |
Hence, from (C.1), an element of length (squared) in the 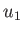 ,
, 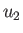 ,
, 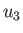 coordinate system is written
coordinate system is written
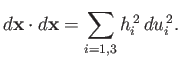 |
(C.6) |
Here, the  , which are generally functions of position, are known as the scale factors of the system.
Elements of area that are normal to
, which are generally functions of position, are known as the scale factors of the system.
Elements of area that are normal to 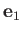 ,
,  , and
, and  , at a given point in space, take the form
, at a given point in space, take the form
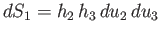 ,
,
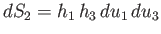 , and
, and
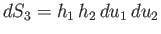 , respectively. Finally, an element of
volume, at a given point in space, is written
, respectively. Finally, an element of
volume, at a given point in space, is written
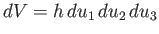 , where
, where
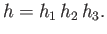 |
(C.7) |
It can be seen that [see Equation (A.176)]
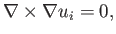 |
(C.8) |
and
 |
(C.9) |
The latter result follows from Equations (A.175) and (A.176) because
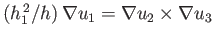 ,
et cetera. Finally, it is easily demonstrated from Equations (C.1) and (C.3) that
,
et cetera. Finally, it is easily demonstrated from Equations (C.1) and (C.3) that
Consider a scalar field
 . It follows from the chain rule, and the relation
. It follows from the chain rule, and the relation
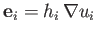 ,
that
,
that
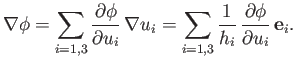 |
(C.12) |
Hence, the components of
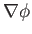 in the
in the 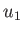 ,
, 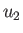 ,
, 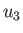 coordinate system are
coordinate system are
 |
(C.13) |
Consider a vector field
 . We can write
. We can write
where use has been made of Equations (A.174), (C.9), and (C.10). Thus, the
divergence of 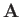 in the
in the 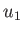 ,
, 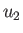 ,
, 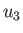 coordinate system takes the form
coordinate system takes the form
 |
(C.15) |
We can write
where use has been made of Equations (A.178), (C.8), and (C.12).
It follows from Equation (C.11) that
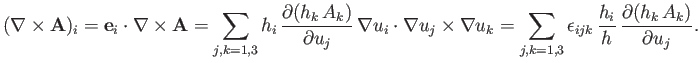 |
(C.17) |
Hence, the components of
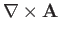 in the
in the
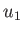 ,
, 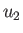 ,
, 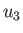 coordinate system are
coordinate system are
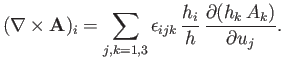 |
(C.18) |
Now,
 [see Equation (A.172)], so Equations (C.12) and (C.15)
yield the following expression for
[see Equation (A.172)], so Equations (C.12) and (C.15)
yield the following expression for
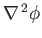 in the
in the 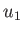 ,
, 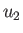 ,
, 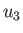 coordinate system:
coordinate system:
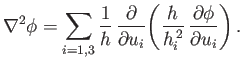 |
(C.19) |
The vector identities (A.171) and (A.179) can be combined to give the
following expression for
 that is valid in a general coordinate system:
that is valid in a general coordinate system:
Making use of Equations (C.13), (C.15), and (C.18), as well
as the easily demonstrated results
and the tensor identity (B.16), Equation (C.20) reduces (after a great deal of tedious algebra) to the
following expression for the components of
 in the
in the 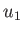 ,
, 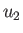 ,
, 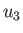 coordinate system:
coordinate system:
![$\displaystyle [({\bf A}\cdot\nabla)\,{\bf B}]_i= \sum_{j=1,3}\left(\frac{A_j}{h...
...ial u_i} + \frac{A_i\,B_j}{h_i\,h_j}\,\frac{\partial h_i}{\partial u_j}\right).$](img7085.png) |
(C.23) |
Note, incidentally, that the commonly quoted result
![$ [({\bf A}\cdot\nabla)\,{\bf B}]_i={\bf A}\cdot\nabla B_i$](img7086.png) is only valid in Cartesian coordinate systems (for which
is only valid in Cartesian coordinate systems (for which
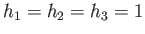 ).
).
Let us define the gradient
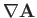 of a vector field
of a vector field 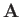 as the tensor whose components in a Cartesian coordinate
system take the form
as the tensor whose components in a Cartesian coordinate
system take the form
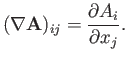 |
(C.24) |
In an orthogonal curvilinear coordinate system, the previous
expression generalizes to
![$\displaystyle (\nabla{\bf A})_{ij} = [({\bf e}_j\cdot\nabla)\,{\bf A}]_i.$](img7090.png) |
(C.25) |
It thus follows from Equation (C.23), and the relation
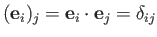 , that
, that
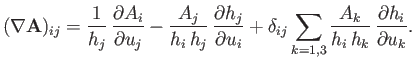 |
(C.26) |
The vector identity (A.177) yields the
following expression for
 that is valid in a general coordinate system:
that is valid in a general coordinate system:
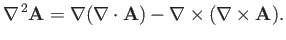 |
(C.27) |
Making use of Equations (C.15), (C.18), and (C.19), as well
as (C.21) and (C.22), and the tensor identity (B.16), the previous equation reduces (after a great deal of
tedious algebra) to the following expression for the components of
 in the
in the 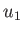 ,
, 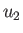 ,
, 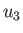 coordinate system:
coordinate system:
Note, again, that the commonly quoted result
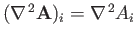 is only valid in Cartesian coordinate systems (for which
is only valid in Cartesian coordinate systems (for which
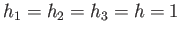 ).
).



Next: Cylindrical Coordinates
Up: Non-Cartesian Coordinates
Previous: Introduction
Richard Fitzpatrick
2016-01-22
![]() ,
,
![]() , and
, and
![]() . It follows that
. It follows that
![]() ,
,
![]() , and
, and
![]() are
a set of unit basis vectors that are normal to surfaces of constant
are
a set of unit basis vectors that are normal to surfaces of constant ![]() ,
, ![]() , and
, and ![]() , respectively, at all points
in space. Note, however, that the direction of these basis vectors is generally a function of position. Suppose that
the
, respectively, at all points
in space. Note, however, that the direction of these basis vectors is generally a function of position. Suppose that
the ![]() , where
, where ![]() runs from 1 to 3, are mutually orthogonal at all points in space: that is,
runs from 1 to 3, are mutually orthogonal at all points in space: that is,

![]() ,
, ![]() ,
, ![]() system are
system are ![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() ,
, ![]() .
It is easily shown that the vector directed from the first to the second of these points takes the form
.
It is easily shown that the vector directed from the first to the second of these points takes the form
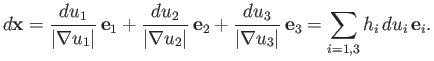
![]() . It follows from the chain rule, and the relation
. It follows from the chain rule, and the relation
![]() ,
that
,
that
![]() . We can write
. We can write
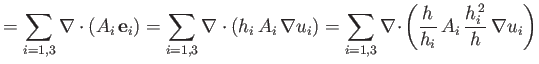

![]() [see Equation (A.172)], so Equations (C.12) and (C.15)
yield the following expression for
[see Equation (A.172)], so Equations (C.12) and (C.15)
yield the following expression for
![]() in the
in the ![]() ,
, ![]() ,
, ![]() coordinate system:
coordinate system:
![]() that is valid in a general coordinate system:
that is valid in a general coordinate system:
![]() of a vector field
of a vector field ![]() as the tensor whose components in a Cartesian coordinate
system take the form
as the tensor whose components in a Cartesian coordinate
system take the form
![]() that is valid in a general coordinate system:
that is valid in a general coordinate system: