


Next: Hemispherical Ocean Tides
Up: Terrestrial Ocean Tides
Previous: Gyroscopic Coefficients
We can automatically satisfy the boundary condition (12.209) by writing
 |
(12.281) |
Likewise, we can automatically satisfy the boundary condition (12.210) by writing
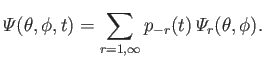 |
(12.282) |
It follows from Equations (12.211), (12.212), (12.227), and (12.235) that
Let
where use has been made of Equations (12.235) and (12.236).
It follows from Equations (12.217) and (12.218) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.216).
Hence, we are left with
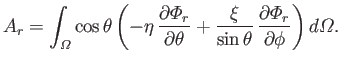 |
(12.289) |
Finally, Equations (12.276), (12.282), (12.288), and (12.289) can be combined with the previous equation to give
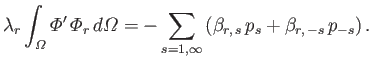 |
(12.290) |
Let
where use has been made of Equations (12.216) and (12.248).
It follows from Equations (12.217) and (12.218) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.249).
Hence, we are left with
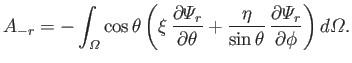 |
(12.293) |
Finally, Equations (12.279), (12.285), (12.288), and (12.289) can be combined with the previous equation to give
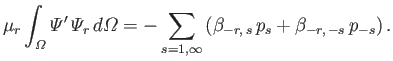 |
(12.294) |
Operating on Equations (12.228) and (12.229) with
 and with
and with
 , respectively, yields the so-called Proudman equations (Proudman 1916):
, respectively, yields the so-called Proudman equations (Proudman 1916):
where
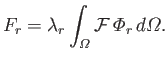 |
(12.297) |
Here, use has been made of Equations (12.240), (12.244), (12.250), (12.286), (12.287), (12.290), (12.295), and (12.299).
Finally, it follows from Equations (12.138), (12.189), and (12.290) that
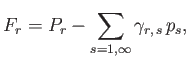 |
(12.298) |
where
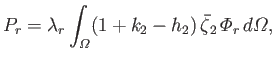 |
(12.299) |
and
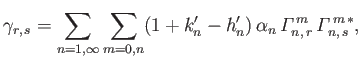 |
(12.300) |
with
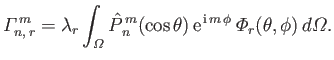 |
(12.301) |
Here,
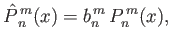 |
(12.302) |
where
![$\displaystyle b_n^{\,m} = \left[\frac{2\,n+1}{4\pi}\,\frac{(n-m)!}{(n+m)!}\right]^{1/2}.$](img4918.png) |
(12.303) |
It follows from Equation (12.136) that
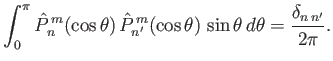 |
(12.304) |
Consider the response of the ocean to a particular harmonic of the tide generating potential for which
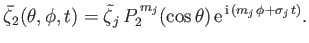 |
(12.305) |
Assuming a common
 time dependence of the
time dependence of the 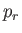 and the
and the 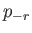 , Equations (12.300) and (12.301) yield
, Equations (12.300) and (12.301) yield
and
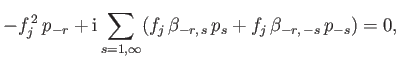 |
(12.306) |
where 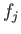 and
and 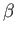 are defined in Equations (12.173) and (12.174), respectively.
are defined in Equations (12.173) and (12.174), respectively.
The task in hand (see Section 12.13) is to solve the Laplace tidal equations, (12.186)-(12.189), subject to the
constraint (12.190). Our basic approach is to expand the fields appearing in the Laplace tidal equations--namely, 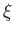 ,
, 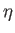 , and
, and
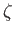 --in terms of a set of basis eigenfunctions--the
--in terms of a set of basis eigenfunctions--the
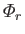 and the
and the
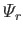 (see Section 12.17)--that are defined in such a
manner as to automatically
satisfy the boundary conditions. The expansion is specified in Equations (12.288)-(12.290). The
Laplace tidal equations then reduce to the Proudman equations, (12.300)-(12.301), which are a set of
coupled ordinary differential equations for the weights in the expansion--the
(see Section 12.17)--that are defined in such a
manner as to automatically
satisfy the boundary conditions. The expansion is specified in Equations (12.288)-(12.290). The
Laplace tidal equations then reduce to the Proudman equations, (12.300)-(12.301), which are a set of
coupled ordinary differential equations for the weights in the expansion--the 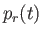 and the
and the 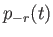 .
For a particular harmonic of the tide generating potential, the weights all oscillate at the same frequency, and the Proudman equations reduce further to give two coupled matrix
equations for the amplitudes of the weights--see Equations (12.311) and (12.312).
In order to solve the matrix equations, we need to calculate the gyroscopic coefficients,
.
For a particular harmonic of the tide generating potential, the weights all oscillate at the same frequency, and the Proudman equations reduce further to give two coupled matrix
equations for the amplitudes of the weights--see Equations (12.311) and (12.312).
In order to solve the matrix equations, we need to calculate the gyroscopic coefficients,
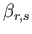 ,
,
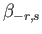 ,
,
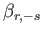 ,
,
 ,
as well as the
,
as well as the
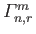 . These quantities are integrals involving the eigenfunctions and the associated Legendre functions, and
are defined in Equations (12.276), (12.279), (12.282), (12.285), and (12.306), respectively.
. These quantities are integrals involving the eigenfunctions and the associated Legendre functions, and
are defined in Equations (12.276), (12.279), (12.282), (12.285), and (12.306), respectively.



Next: Hemispherical Ocean Tides
Up: Terrestrial Ocean Tides
Previous: Gyroscopic Coefficients
Richard Fitzpatrick
2016-01-22

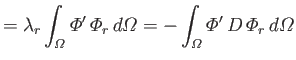
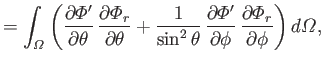

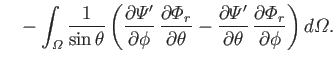
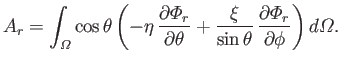
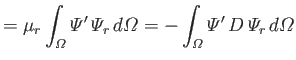

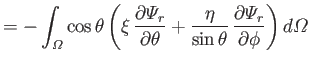
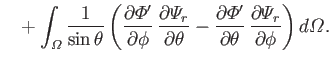
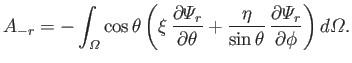
![]() and with
and with
![]() , respectively, yields the so-called Proudman equations (Proudman 1916):
, respectively, yields the so-called Proudman equations (Proudman 1916):
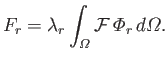
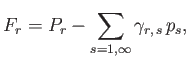
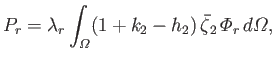
![$\displaystyle b_n^{\,m} = \left[\frac{2\,n+1}{4\pi}\,\frac{(n-m)!}{(n+m)!}\right]^{1/2}.$](img4918.png)
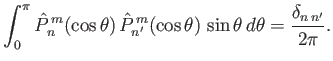
![]() ,
, ![]() , and
, and
![]() --in terms of a set of basis eigenfunctions--the
--in terms of a set of basis eigenfunctions--the
![]() and the
and the
![]() (see Section 12.17)--that are defined in such a
manner as to automatically
satisfy the boundary conditions. The expansion is specified in Equations (12.288)-(12.290). The
Laplace tidal equations then reduce to the Proudman equations, (12.300)-(12.301), which are a set of
coupled ordinary differential equations for the weights in the expansion--the
(see Section 12.17)--that are defined in such a
manner as to automatically
satisfy the boundary conditions. The expansion is specified in Equations (12.288)-(12.290). The
Laplace tidal equations then reduce to the Proudman equations, (12.300)-(12.301), which are a set of
coupled ordinary differential equations for the weights in the expansion--the ![]() and the
and the ![]() .
For a particular harmonic of the tide generating potential, the weights all oscillate at the same frequency, and the Proudman equations reduce further to give two coupled matrix
equations for the amplitudes of the weights--see Equations (12.311) and (12.312).
In order to solve the matrix equations, we need to calculate the gyroscopic coefficients,
.
For a particular harmonic of the tide generating potential, the weights all oscillate at the same frequency, and the Proudman equations reduce further to give two coupled matrix
equations for the amplitudes of the weights--see Equations (12.311) and (12.312).
In order to solve the matrix equations, we need to calculate the gyroscopic coefficients,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
as well as the
,
as well as the
![]() . These quantities are integrals involving the eigenfunctions and the associated Legendre functions, and
are defined in Equations (12.276), (12.279), (12.282), (12.285), and (12.306), respectively.
. These quantities are integrals involving the eigenfunctions and the associated Legendre functions, and
are defined in Equations (12.276), (12.279), (12.282), (12.285), and (12.306), respectively.