


Next: Proudman Equations
Up: Terrestrial Ocean Tides
Previous: Auxilliary Eigenfunctions
Gyroscopic Coefficients
Let
where use has been made of Equations (12.235) and (12.236). It follows from Equations (12.262) and (12.263) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.261). Hence, we are left with
 |
(12.271) |
Let
where use has been made of Equations (12.235) and (12.236). It follows from Equations (12.272) and (12.273) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.271). Hence, we are left with
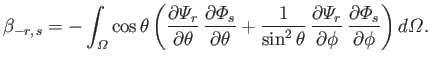 |
(12.274) |
Let
where use has been made of Equations (12.248) and (12.261). It follows from Equations (12.262) and (12.263) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.249). Hence, we are left with
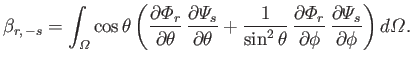 |
(12.277) |
Finally, let
where use has been made of Equations (12.248) and (12.271). It follows from Equations (12.272) and (12.273) that
However, the second term on the right-hand side of the previous equation integrates to zero with the aid of Equation (12.249). Hence, we are left with
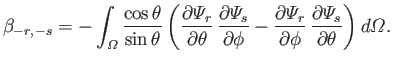 |
(12.280) |
Incidentally, the
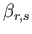 ,
,
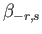 ,
,
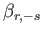 , and
, and
 are known collectively as gyroscopic coefficients (Proudman 1916).
are known collectively as gyroscopic coefficients (Proudman 1916).



Next: Proudman Equations
Up: Terrestrial Ocean Tides
Previous: Auxilliary Eigenfunctions
Richard Fitzpatrick
2016-01-22




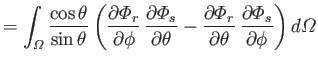

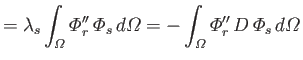
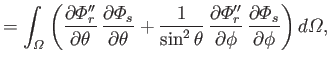
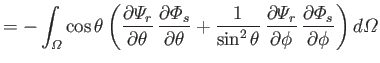

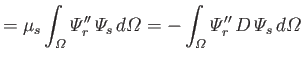
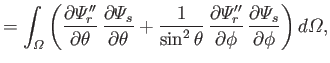
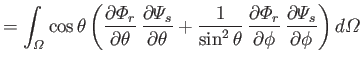
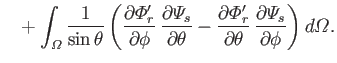
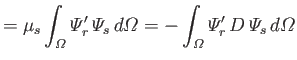

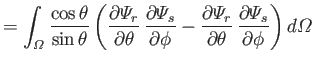
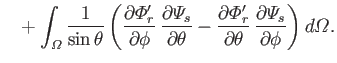
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are known collectively as gyroscopic coefficients (Proudman 1916).
are known collectively as gyroscopic coefficients (Proudman 1916).