

Next: 3-d problems
Up: The diffusion equation
Previous: An example 2-d diffusion
Let us now solve the diffusion equation in 2-d using the finite difference technique discussed above.
We seek the solution of Eq. (214) in the region 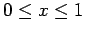 and
and
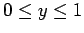 , subject to the following initial condition at
, subject to the following initial condition at 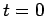 :
:
The boundary conditions are simply
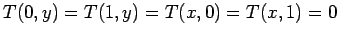 .
.
Figure 74:
Diffusion in two dimensions.
Numerical calculation performed using
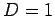 ,
,
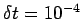 , and
, and 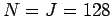 . Density plots of
. Density plots of 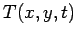 are shown at
are shown at
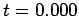 (top-left),
(top-left), 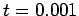 (top-right),
(top-right), 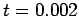 (middle-left),
(middle-left),  (middle-right),
(middle-right),  (bottom-left), and
(bottom-left), and  (bottom-right).
(bottom-right).
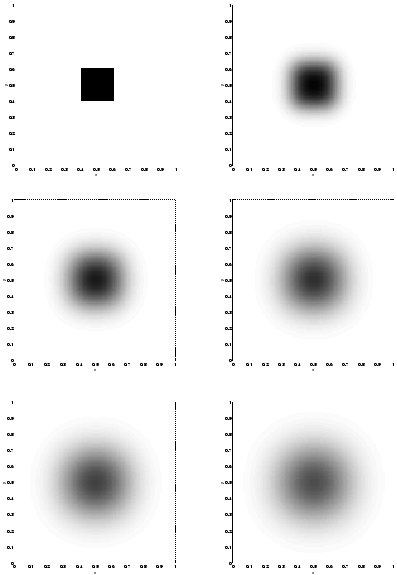 |
Figure 74 shows the evolution of 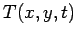 for a calculation performed
with the previously listed 2-d diffusion equation solver
using
for a calculation performed
with the previously listed 2-d diffusion equation solver
using 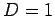 ,
,
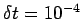 , and
, and 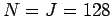 .
.


Next: 3-d problems
Up: The diffusion equation
Previous: An example 2-d diffusion
Richard Fitzpatrick
2006-03-29

![]() for a calculation performed
with the previously listed 2-d diffusion equation solver
using
for a calculation performed
with the previously listed 2-d diffusion equation solver
using ![]() ,
,
![]() , and
, and ![]() .
.