| (45) | |||
| (46) | |||
| (47) | |||
| (48) | |||
| (49) | |||
| (50) |
| (45) | |||
| (46) | |||
| (47) | |||
| (48) | |||
| (49) | |||
| (50) |
| (51) | |||
| (52) | |||
| (53) | |||
| (54) | |||
| (55) | |||
| (56) |
The above set of equations have been solved numerically using a fixed step-length, fourth-order
Runge-Kutta method. The step-length, h, is conveniently expressed as a fraction of the
pitch's estimated
time-of-flight, ![]() , where
, where
![]() is the horizontal
distance between the pitcher and the hitter. Thus, 1/h is approximately the number
of steps used to integrate the trajectory.
is the horizontal
distance between the pitcher and the hitter. Thus, 1/h is approximately the number
of steps used to integrate the trajectory.
It is helpful, at this stage, to describe the conventional classification of baseball pitches in terms of the direction of the ball's axis of spin. Figure 13 shows the direction of rotation of various different pitches thrown by a right-handed pitcher, as seen by the hitter. Obviously, the directions are reversed for the corresponding pitches thrown by a left-handed pitcher. Note, from Eq. (43), that the arrows in Fig. 13 show both the direction of the ball's spin and the direction of the Magnus force.
 |
Figure 14 shows the numerical trajectory of a ``slider'' delivered
by a right-handed pitcher. The ball is thrown such that its axis
of rotation points vertically upwards, which is the direction of spin generated by
the natural clockwise (seen from below) rotation of a right-handed pitcher's wrist.
The associated Magnus force causes the
ball to curve sideways, away from a right-handed hitter (i.e., in the
![]() -direction). As can be seen, from the figure, the sideways displacement
for an 85mph pitch spinning at
1800rpm is over 1 foot. Of course, a slider delivered
by a left-handed pitcher would curve towards a right-handed hitter.
It turns out that pitches which curve towards a hitter are far harder to
hit than pitches which curve away. Thus, a right-handed
hitter is at a distinct disadvantage when facing a left-handed pitcher, and
vice versa. A lot of strategy in baseball games is
associated with teams trying to match the handedness of hitters and
pitchers so as to gain an advantage over their opponents.
-direction). As can be seen, from the figure, the sideways displacement
for an 85mph pitch spinning at
1800rpm is over 1 foot. Of course, a slider delivered
by a left-handed pitcher would curve towards a right-handed hitter.
It turns out that pitches which curve towards a hitter are far harder to
hit than pitches which curve away. Thus, a right-handed
hitter is at a distinct disadvantage when facing a left-handed pitcher, and
vice versa. A lot of strategy in baseball games is
associated with teams trying to match the handedness of hitters and
pitchers so as to gain an advantage over their opponents.
 |
Figure 14 shows the numerical trajectory of a ``curveball'' delivered by a right-handed pitcher. The ball is thrown such that its axis of rotation, as seen by the hitter, points upwards, but also tilts to the right. The hand action associated with throwing a curveball is actually somewhat more natural than that associated with a slider. The Magnus force acting on a curveball causes the ball to deviate both sideways and downwards. Thus, although a curveball generally does not move laterally as far as a slider, it dips unusually rapidly--which makes it difficult to hit. The anomalously large dip of a typical curveball is apparent from a comparison of Figs. 14 and 15.
 |
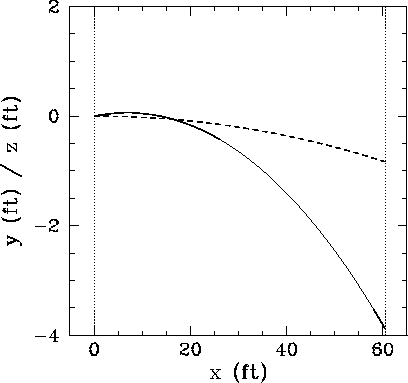
As we have already mentioned, a pitch which curves towards a hitter is harder to hit than one which curves away. It is actually possible for a right-handed pitcher to throw an inward curving pitch to a right-handed hitter. Such a pitch is known as a ``screwball.'' Unfortunately, throwing screwballs involves a completely unnatural wrist rotation which is extremely difficult to master. Figure 16 shows the numerical trajectory of a screwball delivered by a right-handed pitcher. The ball is thrown such that its axis of rotation, as seen by the hitter, points upwards and tilts to the left. Note that the pitch dips rapidly--like a curveball--but has a sideways displacement in the opposite direction to normal.
 |
Probably the most effective pitch in baseball is the so-called ``fastball.''
As the name suggests, a fastball is thrown extremely rapidly--typically,
at ![]() mph. The natural hand action associated with throwing this
type of pitch tends to impart a significant amount of backspin to the
ball. Thus, the Magnus force acting on a fastball has a large
upwards component, slowing the ball's rate of fall.
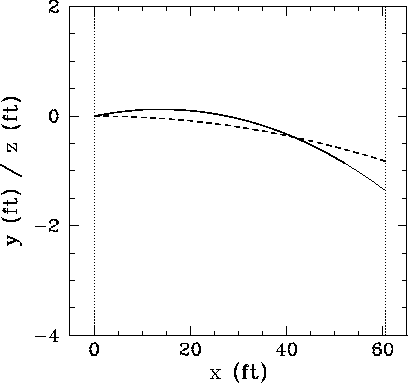
Figure 17 shows the numerical trajectory of a fastball delivered
by a right-handed pitcher. The ball is thrown such that its
axis of rotation, as seen by the hitter,
points downwards and tilts to the left.
Note that the pitch falls an unusually small distance. This is partly because the ball takes
less time than normal to reach the hitter, but partly also because the Magnus force has a
substantial upward component. This type of pitch is often called
a ``rising fastball,'' because hitters often claim that the ball rises
as it moves towards them. Actually, this is
an optical illusion created by the ball's smaller than expected rate of fall.
mph. The natural hand action associated with throwing this
type of pitch tends to impart a significant amount of backspin to the
ball. Thus, the Magnus force acting on a fastball has a large
upwards component, slowing the ball's rate of fall.
Figure 17 shows the numerical trajectory of a fastball delivered
by a right-handed pitcher. The ball is thrown such that its
axis of rotation, as seen by the hitter,
points downwards and tilts to the left.
Note that the pitch falls an unusually small distance. This is partly because the ball takes
less time than normal to reach the hitter, but partly also because the Magnus force has a
substantial upward component. This type of pitch is often called
a ``rising fastball,'' because hitters often claim that the ball rises
as it moves towards them. Actually, this is
an optical illusion created by the ball's smaller than expected rate of fall.
 |