The Magnus force

We have not yet explained how a baseball is able to curve through the air. Physicists in the last century could not account for this effect, and actually tried to dismiss it as an ``optical illusion.'' It turns out that this strange phenomenon is associated with the fact that the balls thrown in major league games tend to spin fairly rapidly--typically, at 1500rpm.

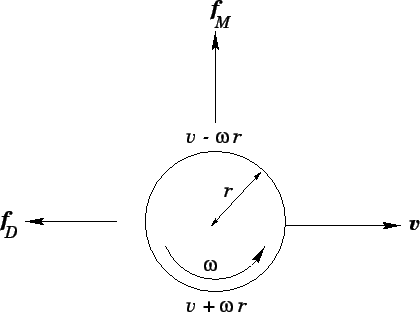
The origin of the force which makes a spinning baseball curve can readily be appreciated once we recall that the drag force acting on a baseball increases with increasing speed.²²For a ball spinning about an axis perpendicular to its direction of travel, the speed of the ball, relative to the air, is different on opposite sides of the ball, as illustrated in Fig. 12. It can be seen, from the diagram, that the lower side of the ball has a larger speed relative to the air than the upper side. This results in a larger drag force acting on the lower surface of the ball than on the upper surface. If we think of drag forces as exerting a sort of pressure on the ball then we can readily appreciate that when the unequal drag forces acting on the ball's upper and lower surfaces are added together there is a component of the resultant force acting upwards. This force--which is known as the Magnus force, after the German physicist Heinrich Magnus, who first described it in 1853--is the dominant spin-dependent force acting on baseballs. The Magnus force can be written

$${\bf f}_M = S(v)\,{\mbox{\boldmath$\omega$}}\times{\bf v},$$ (43)

where ${\mbox{\boldmath$\omega$}}$ is the angular velocity vector of the ball. According to Adair and Giordano, it is a fairly good approximation to take

$$B= \frac{S}{m} = 4.1\times 10^{-4}$$ (44)

for baseballs. Note that $B$ is a dimensionless quantity. The magnitude of the Magnus force is about one third of the force due to gravity for typical curveballs.

Figure 12: Origin of the Magnus force for a ball of radius $r$, moving with speed $v$, and spinning with angular velocity $\omega$ about an axis perpendicular to its direction of motion.