


Next: Inductance
Up: Magnetic Induction
Previous: Worked Example 4: AC
Question: An AC motor has an internal resistance of  . When
powered by a
. When
powered by a 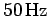 AC supply of peak voltage
AC supply of peak voltage
 it draws a peak current of
it draws a peak current of
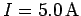 . What is the peak back-emf produced by the motor? What is the peak power
delivered to the motor by the AC supply? What is the peak rate of energy loss as heat in the
motor? What is the peak useful power produced by the motor? What is the efficiency
(i.e., the ratio of the peak useful power output to the peak power delivered)
of such a motor?
. What is the peak back-emf produced by the motor? What is the peak power
delivered to the motor by the AC supply? What is the peak rate of energy loss as heat in the
motor? What is the peak useful power produced by the motor? What is the efficiency
(i.e., the ratio of the peak useful power output to the peak power delivered)
of such a motor?
Answer: If 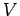 is the peak applied voltage, and
is the peak applied voltage, and 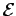 the peak back-emf, then the peak applied voltage must equal the sum of the peak voltage
drops across the motor, or
the peak back-emf, then the peak applied voltage must equal the sum of the peak voltage
drops across the motor, or
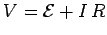 . It follows that
. It follows that
The peak power delivered by the AC supply is
Energy is lost as heat in the motor at the peak rate
The peak useful power produced by the motor is the difference between the
peak power supplied to the motor and the peak power dissipated as heat:
The peak useful power is also given by the product of the peak back-emf and
the peak current flowing through the motor [see Eq. (226)],
The efficiency 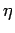 is the ratio of the peak useful power output of the motor
to the peak power supplied, or
is the ratio of the peak useful power output of the motor
to the peak power supplied, or



Next: Inductance
Up: Magnetic Induction
Previous: Worked Example 4: AC
Richard Fitzpatrick
2007-07-14