


Next: Worked Example 4: AC
Up: Magnetic Induction
Previous: Worked Example 2: Lenz's
Question: Consider the circuit described in Sect. 9.4.
Suppose that the length of the moving rod is 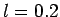 m, its speed
is
m, its speed
is
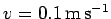 , the magnetic field-strength is
, the magnetic field-strength is 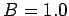 T
(the field is directed into the page--see Fig. 36), and the resistance of the circuit is
T
(the field is directed into the page--see Fig. 36), and the resistance of the circuit is
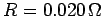 . What is the emf generated around the circuit? What current
flows around the circuit? What is the magnitude and direction of the force
acting on the moving rod due to the fact that a current is flowing along it?
What is the rate at which work must be performed on the rod in order to
keep it moving at constant velocity against this force? What is the rate at
which electrical energy is generated? What is the rate at which energy is converted
into heat due to the resistivity of the circuit?
. What is the emf generated around the circuit? What current
flows around the circuit? What is the magnitude and direction of the force
acting on the moving rod due to the fact that a current is flowing along it?
What is the rate at which work must be performed on the rod in order to
keep it moving at constant velocity against this force? What is the rate at
which electrical energy is generated? What is the rate at which energy is converted
into heat due to the resistivity of the circuit?
Answer: The emf is generated by the motion of the rod. According to
Eq. (204), the magnitude of the motional emf is
The emf acts in the anti-clockwise direction in Fig. 36.
The anti-clockwise current driven around the circuit by the motional
emf follows from Ohm's law:
Since the rod carries a current  which flows perpendicular to a magnetic
field
which flows perpendicular to a magnetic
field 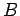 , the force per unit length acting on the rod is
, the force per unit length acting on the rod is
 (see Sect. 8.2). Thus, the total force acting on the rod is of magnitude
(see Sect. 8.2). Thus, the total force acting on the rod is of magnitude
This force is directed parallel to the vector
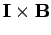 .
It follows that the force is to the left in Fig. 36. In other words, the force opposes the motion producing the
emf.
.
It follows that the force is to the left in Fig. 36. In other words, the force opposes the motion producing the
emf.
In order to keep the rod moving at a constant velocity, some external
agent must apply a force to the rod which is equal and opposite to
the magnetic force described above. Thus, the externally applied force acts to
the right.
The rate  at which work is done
by this force is the product of the force and the velocity of the rod in the
direction of this force. Thus,
at which work is done
by this force is the product of the force and the velocity of the rod in the
direction of this force. Thus,
Every charge 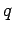 which circulates around the circuit in the anti-clockwise
direction acquires the energy
which circulates around the circuit in the anti-clockwise
direction acquires the energy 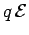 . The amount of charge per unit
time which circulates around the circuit is, by definition, equal to the
current
. The amount of charge per unit
time which circulates around the circuit is, by definition, equal to the
current  flowing around the circuit. Thus, the rate at which electric charges
acquire energy in the circuit is
flowing around the circuit. Thus, the rate at which electric charges
acquire energy in the circuit is
Now, the rate at which electric charges acquire energy in the circuit is equal
to the rate at which mechanical work is done on the rod by the
external force, as must be the case if energy is to
be conserved. Thus, we can think of this circuit as constituting a
primitive generator which transforms mechanical into electrical
energy.
The rate at which electrical energy is converted into heat energy in the
circuit is
Thus, all of the mechanical work done on the rod eventually ends up as heat dissipated
in the circuit.



Next: Worked Example 4: AC
Up: Magnetic Induction
Previous: Worked Example 2: Lenz's
Richard Fitzpatrick
2007-07-14
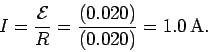
![]() which flows perpendicular to a magnetic
field
which flows perpendicular to a magnetic
field ![]() , the force per unit length acting on the rod is
, the force per unit length acting on the rod is
![]() (see Sect. 8.2). Thus, the total force acting on the rod is of magnitude
(see Sect. 8.2). Thus, the total force acting on the rod is of magnitude
![]() at which work is done
by this force is the product of the force and the velocity of the rod in the
direction of this force. Thus,
at which work is done
by this force is the product of the force and the velocity of the rod in the
direction of this force. Thus,
![]() which circulates around the circuit in the anti-clockwise
direction acquires the energy
which circulates around the circuit in the anti-clockwise
direction acquires the energy ![]() . The amount of charge per unit
time which circulates around the circuit is, by definition, equal to the
current
. The amount of charge per unit
time which circulates around the circuit is, by definition, equal to the
current ![]() flowing around the circuit. Thus, the rate at which electric charges
acquire energy in the circuit is
flowing around the circuit. Thus, the rate at which electric charges
acquire energy in the circuit is