

Next: Worked Example 3: Motional
Up: Magnetic Induction
Previous: Example 9.1: Faraday's law
Question: A long solenoid with an air core has 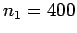 turns per meter
and a cross-sectional area of
turns per meter
and a cross-sectional area of
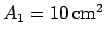 . The current
. The current 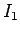 flowing
around
the solenoid increases from 0 to
flowing
around
the solenoid increases from 0 to 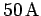 in
in 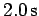 .
A plane loop of wire consisting of
.
A plane loop of wire consisting of 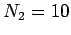 turns, which is of cross-sectional area
turns, which is of cross-sectional area
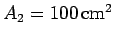 and resistance
and resistance
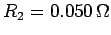 , is placed around the
solenoid close to its centre. The loop is orientated such that
it lies in the plane perpendicular to the axis
of the solenoid.
What is the magnitude
, is placed around the
solenoid close to its centre. The loop is orientated such that
it lies in the plane perpendicular to the axis
of the solenoid.
What is the magnitude 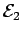 of the emf
induced
in the coil? What current
of the emf
induced
in the coil? What current 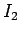 does does this emf drive around the coil?
Does this current circulate in the same direction as the current flowing in
the solenoid, or in the opposite direction?
does does this emf drive around the coil?
Does this current circulate in the same direction as the current flowing in
the solenoid, or in the opposite direction?
Answer: We must, first of all, calculate the magnetic
flux linking the coil. The magnetic field is confined to the region
inside the solenoid (the field generated outside a long solenoid
is essentially negligible). The magnetic field runs along the axis of the
solenoid, so it is directed perpendicular to the plane of the coil. Thus,
the magnetic flux linking a single turn of the coil is the product of the
area 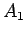 of the magnetic-field-containing region and the strength
of the magnetic-field-containing region and the strength 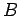 of the perpendicular field. Note that, in this case, the magnetic flux does
not depend on the area
of the perpendicular field. Note that, in this case, the magnetic flux does
not depend on the area 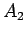 of the coil, as long as the magnetic-field-containing
region lies completely within the coil.
The magnetic flux
of the coil, as long as the magnetic-field-containing
region lies completely within the coil.
The magnetic flux 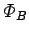 linking the
whole coil is the flux linking a single turn times the number
linking the
whole coil is the flux linking a single turn times the number 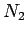 of
turns in the coil. Thus,
of
turns in the coil. Thus,
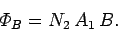
Now, the magnitude of the magnetic field generated by the solenoid
is given by (see Sect. 8.8)
so the magnetic flux linking the coil can be written
This magnetic flux increases because the current 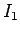 flowing in the
solenoid increases.
Thus, the time rate of change of the magnetic flux is given by
flowing in the
solenoid increases.
Thus, the time rate of change of the magnetic flux is given by
By Faraday's induction law, the emf generated around the coil is
Ohm's law gives
as the current induced in the coil.
According to Lenz's law, the current induced in the coil is such as to
oppose the increase in the magnetic flux linking the coil. Thus, the current
in the coil must circulate in the opposite direction to the current in
the solenoid, so that the magnetic field generated by the the former current, in the middle of
the coil, is oppositely directed to that generated by the latter current.
The fact that the current 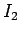 in the above formula is negative
is indicative of the fact that
this current
runs in the opposite direction to the current flowing around the solenoid.
in the above formula is negative
is indicative of the fact that
this current
runs in the opposite direction to the current flowing around the solenoid.


Next: Worked Example 3: Motional
Up: Magnetic Induction
Previous: Example 9.1: Faraday's law
Richard Fitzpatrick
2007-07-14
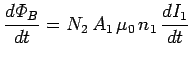
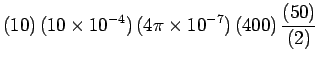
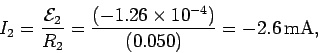
![]() in the above formula is negative
is indicative of the fact that
this current
runs in the opposite direction to the current flowing around the solenoid.
in the above formula is negative
is indicative of the fact that
this current
runs in the opposite direction to the current flowing around the solenoid.