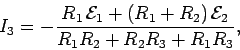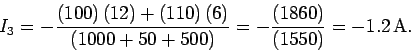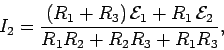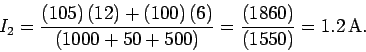Next: Example 7.4: Energy in
Up: Electric Current
Previous: Example 7.2: Equivalent resistance
Question:
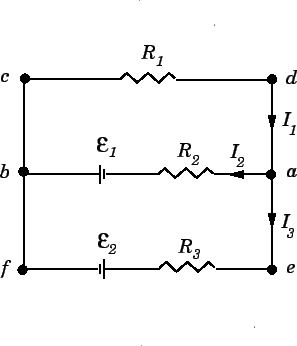
Find the three currents 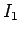 ,
, 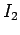 , and
, and 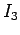 in the circuit shown in the diagram,
where
in the circuit shown in the diagram,
where
 ,
,
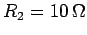 ,
, 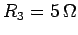 ,
, 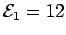 V
and
V
and 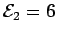 V.
V.
Answer: Applying the junction rule to point 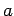 , and assuming that
the currents flow in the direction shown (the initial choice of
directions of the currents is arbitrary), we have
, and assuming that
the currents flow in the direction shown (the initial choice of
directions of the currents is arbitrary), we have
There is no need to apply the junction rule again at point 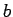 , since if the
above equation is satisfied then this rule is automatically satisfied at
, since if the
above equation is satisfied then this rule is automatically satisfied at 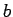 .
.
Let us apply the loop rule by going around the various loops in the circuit
in a clockwise direction. For loop 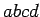 , we have
, we have
Note that both the terms involving resistors are negative, since we cross
the resistors in question in the direction of nominal current flow.
Likewise, the term involving the emf is positive since we traverse the
emf in question from the negative to the positive plate. For loop
 , we find
, we find
There is no need to apply the loop rule to the full loop 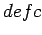 , since
this loop is made up of loops
, since
this loop is made up of loops 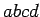 and
and  , and the loop rules for these two
loops therefore already contain all of the information
which would be obtained by applying the
loop rule to
, and the loop rules for these two
loops therefore already contain all of the information
which would be obtained by applying the
loop rule to 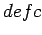 .
.
Combining the junction rule with the first loop rule, we obtain
The second loop rule can be rearranged to give
The above two equations are a pair of simultaneous algebraic equations
for the currents 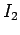 and
and 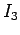 , and can be solved using the standard method
for solving such equations.
Multiplying the first equation by
, and can be solved using the standard method
for solving such equations.
Multiplying the first equation by 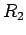 , the second by
, the second by 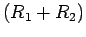 , and adding
the resulting equations, we obtain
, and adding
the resulting equations, we obtain
which can be rearranged to give
or
Likewise, multiplying the first equation by 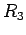 , the second by
, the second by 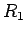 , and
taking the difference of the resulting equations, we obtain
, and
taking the difference of the resulting equations, we obtain
which can be rearranged to give
or
Finally, from the junction rule,
The fact that
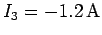 indicates that this current is of magnitude
indicates that this current is of magnitude
 A, but flows in the opposite direction to that which we initially
guessed. In fact, we can see that a current of
A, but flows in the opposite direction to that which we initially
guessed. In fact, we can see that a current of  A circulates in an
anti-clockwise direction in the lower loop of the circuit, whereas zero current
circulates in the upper loop.
A circulates in an
anti-clockwise direction in the lower loop of the circuit, whereas zero current
circulates in the upper loop.



Next: Example 7.4: Energy in
Up: Electric Current
Previous: Example 7.2: Equivalent resistance
Richard Fitzpatrick
2007-07-14
![]() , we have
, we have