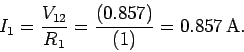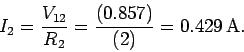Next: Example 7.3: Kirchhoff's rules
Up: Electric Current
Previous: Example 7.1: Ohm's law
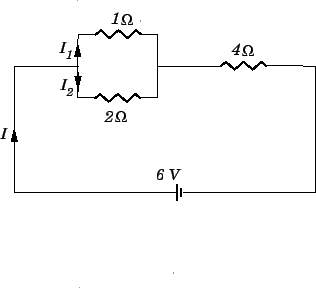
Question: A  and a
and a
 resistor are connected in parallel,
and this pair of resistors is connected in series with a
resistor are connected in parallel,
and this pair of resistors is connected in series with a  resistor.
What is the equivalent resistance of the whole combination? What is the
current flowing through the
resistor.
What is the equivalent resistance of the whole combination? What is the
current flowing through the 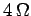 resistor if the whole combination is
connected across the terminals of a
resistor if the whole combination is
connected across the terminals of a  battery (of negligible
internal resistance)? Likewise, what are the currents flowing through the
battery (of negligible
internal resistance)? Likewise, what are the currents flowing through the
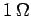 and
and 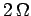 resistors?
resistors?
Answer: The equivalent resistance of the
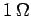 and
and 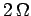 resistors is
resistors is
giving
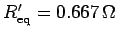 . When a
. When a
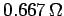 resistor is combined in series with a
resistor is combined in series with a 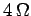 resistor, the
equivalent resistance is
resistor, the
equivalent resistance is
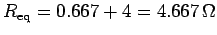 .
.
The current driven by the  battery is
battery is
This is the current flowing through the 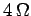 resistor, since one end of
this resistor is connected directly to the battery, with no intermediate
junction points.
resistor, since one end of
this resistor is connected directly to the battery, with no intermediate
junction points.
The voltage drop across the 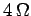 resistor is
resistor is
Thus, the voltage drop across the 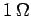 and
and 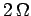 combination is
combination is
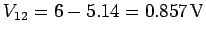 . The current flowing through the
. The current flowing through the 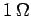 resistor is given by
resistor is given by
Likewise, the current flowing through the 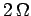 resistor is
resistor is
Note that the total current flowing through the 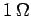 and
and 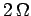 combination is
combination is
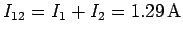 , which is the same as the current flowing through
the
, which is the same as the current flowing through
the 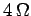 resistor. This makes sense because the
resistor. This makes sense because the 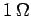 and
and 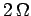 combination
is connected in series with the
combination
is connected in series with the 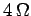 resistor.
resistor.



Next: Example 7.3: Kirchhoff's rules
Up: Electric Current
Previous: Example 7.1: Ohm's law
Richard Fitzpatrick
2007-07-14


![]() battery is
battery is
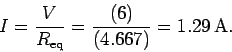
![]() resistor is
resistor is