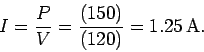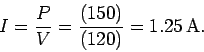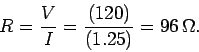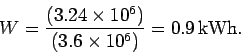Next: Magnetism
Up: Electric Current
Previous: Example 7.3: Kirchhoff's rules
Question: A 150W light bulb is connected to a 120V line.
What is the current drawn from the line? What is the resistance of the light
bulb whilst it is burning? How much energy is consumed if the light is
kept on for 6 hours? What is the cost of this energy at 8 cents/kWh?
Answer: Since power is equal to  , it follows that
, it follows that
From Ohm's law, the resistance of the light bulb is
The energy 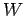 consumed is the product of the power
consumed is the product of the power  (the energy consumed per
unit time) and the time period
(the energy consumed per
unit time) and the time period 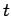 for which the light is on, so
for which the light is on, so
Since,
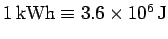 , it
follows that
, it
follows that
The cost 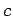 of the electricity is product of the number of kilowatthours used
and the cost per kilowatthour, so
of the electricity is product of the number of kilowatthours used
and the cost per kilowatthour, so



Next: Magnetism
Up: Electric Current
Previous: Example 7.3: Kirchhoff's rules
Richard Fitzpatrick
2007-07-14