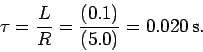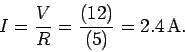Next: Example 10.4: The RC
Up: Inductance
Previous: Example 10.2: Energy density
Question: A coil has a resistance of 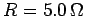 and
an inductance of
and
an inductance of
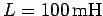 . At a particular instant in time
after a battery is connected across the coil, the current is
. At a particular instant in time
after a battery is connected across the coil, the current is
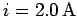 ,
and is increasing at a rate of
,
and is increasing at a rate of
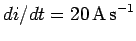 . What is the voltage
. What is the voltage
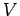 of the battery? What is the time-constant of the circuit? What is
the final value of the current?
of the battery? What is the time-constant of the circuit? What is
the final value of the current?
Answer: Application of Ohm's law around the circuit gives [see Eq. (257)]
The time-constant of the circuit is simply
The final steady-state current  is given by Ohm's law, with the inductor acting
like a conducting wire, so
is given by Ohm's law, with the inductor acting
like a conducting wire, so
Richard Fitzpatrick
2007-07-14