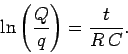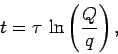Next: Example 10.5: The step-up
Up: Inductance
Previous: Example 10.3: The RL
Question: A capacitor of capacitance
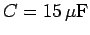 is charged up to a
voltage of
is charged up to a
voltage of
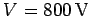 , and then discharged by connecting a
resistor of resistance
, and then discharged by connecting a
resistor of resistance
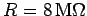 across its terminals. How
long does it take for the charge on the positive plate of the capacitor to
be reduced to
across its terminals. How
long does it take for the charge on the positive plate of the capacitor to
be reduced to 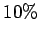 of its original value?
of its original value?
Answer: Suppose that the resistor is first connected across the
capacitor at  . The charge
. The charge 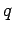 on the positive plate of the capacitor
is given by
on the positive plate of the capacitor
is given by
which can be rearranged to give
Taking the natural logarithm of both sides, we obtain
Hence,
where
is the 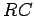 time. Since
time. Since 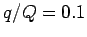 , in this case, it follows that
, in this case, it follows that



Next: Example 10.5: The step-up
Up: Inductance
Previous: Example 10.3: The RL
Richard Fitzpatrick
2007-07-14