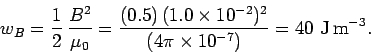Next: Example 10.3: The RL
Up: Inductance
Previous: Example 10.1: Mutual induction
Question: In a certain region of space, the magnetic field has a value
of
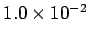 T, and the electric field has a value
of
T, and the electric field has a value
of
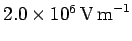 . What is the combined energy density of
the electric and magnetic fields?
. What is the combined energy density of
the electric and magnetic fields?
Answer: For the electric field, the energy density is
For the magnetic field, the energy density is
The net energy density is the sum of the energy density due to the electric
field and the energy density due to the magnetic field:
Richard Fitzpatrick
2007-07-14