Next: Dispersive Waves Up: Wave Pulses Previous: Bandwidth Theorem Contents
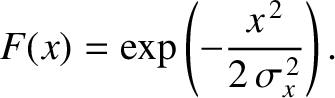
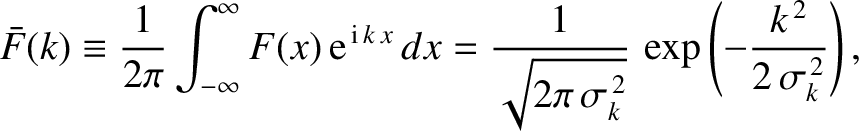
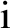 is the square-root of minus one, and
is the square-root of minus one, and
 . [Hint: You
will need to complete the square of the exponent of
. [Hint: You
will need to complete the square of the exponent of 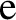 , transform the variable of
integration, and then make use of the standard result that
, transform the variable of
integration, and then make use of the standard result that
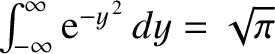 .] Hence, show from Euler's theorem,
.] Hence, show from Euler's theorem,
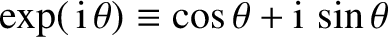 , that
, that
 |
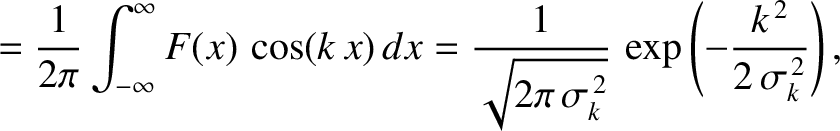 |
|
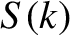 |
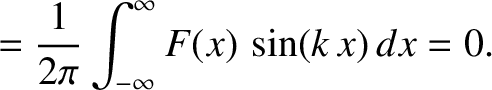 |
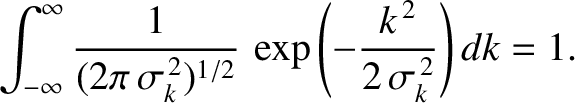
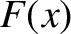 and
and 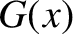 .
.
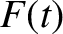 that is zero for negative
that is zero for negative  , and takes the
value
, and takes the
value
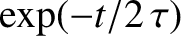 for
for 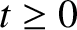 . Find its Fourier transforms,
. Find its Fourier transforms, 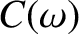 and
and 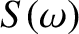 , defined by
, defined by
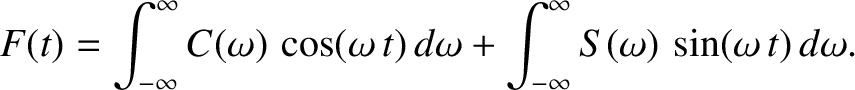
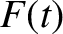 be zero, except in the interval from
be zero, except in the interval from
 to
to
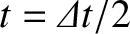 . Suppose that in this
interval
. Suppose that in this
interval 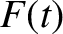 makes exactly one sinusoidal oscillation at the angular frequency
makes exactly one sinusoidal oscillation at the angular frequency
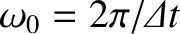 , starting and ending with the value zero. Find the previously defined Fourier transforms
, starting and ending with the value zero. Find the previously defined Fourier transforms 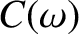 and
and 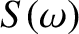 .
.
![$\displaystyle \int_{-\infty}^\infty F^{\,2}(t)\,dt= 2\pi\int_{-\infty}^\infty\left[C^{\,2}(\omega)+S^{\,2}(\omega)\right]d\omega,
$](img2525.png)
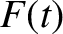 ,
, 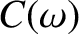 , and
, and 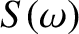 is as previously defined.
This result is known as Parseval's theorem.
is as previously defined.
This result is known as Parseval's theorem.
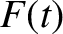 and
and 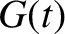 are both even functions of
are both even functions of  with the cosine
transforms
with the cosine
transforms
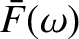 and
and
 , so that
, so that
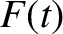 |
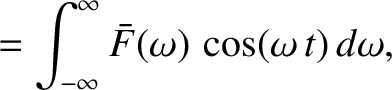 |
|
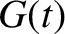 |
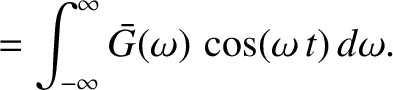 |
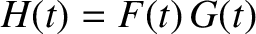 , and let
, and let
 be the cosine transform of
this even function, so that
be the cosine transform of
this even function, so that
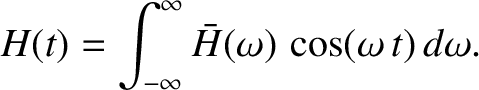
![$\displaystyle \bar{H}(\omega) = \frac{1}{2}\int_{-\infty}^\infty \bar{F}(\omega')\left[\bar{G}(\omega'+\omega) + \bar{G}(\omega'-\omega)\right] d\omega'.
$](img2536.png)
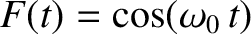 .
Show that
.
Show that
![$\displaystyle \bar{H}(\omega) = \frac{1}{2}\left[\bar{G}(\omega-\omega_0) + \bar{G}(\omega+\omega_0)\right].
$](img2538.png)
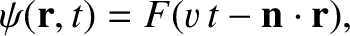
 is an arbitrary function, and
is an arbitrary function, and  a constant unit vector, is a solution of the three-dimensional wave equation, (7.9).
How would you interpret this solution?
a constant unit vector, is a solution of the three-dimensional wave equation, (7.9).
How would you interpret this solution?
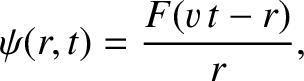
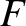 is an arbitrary function,
is a solution of the spherical wave equation, (7.12).
How would you interpret this solution?
is an arbitrary function,
is a solution of the spherical wave equation, (7.12).
How would you interpret this solution?