Next: Exercises Up: Wave Pulses Previous: Bandwidth Contents
Let us now consider how we might transmit a digital signal over AM radio.
Suppose that each data “bit” in the signal takes the form of a Gaussian envelope,
of characteristic duration 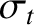 , superimposed on a
carrier wave whose frequency is
, superimposed on a
carrier wave whose frequency is  ; that is,
; that is,
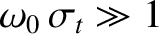 . In other words, the period of the
carrier wave is much less than the duration of the bit.
Figure 8.5 illustrates a digital bit calculated for
. In other words, the period of the
carrier wave is much less than the duration of the bit.
Figure 8.5 illustrates a digital bit calculated for
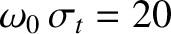 .
.
The sine Fourier transform of the signal (8.68) is zero by symmetry. However, its cosine Fourier transform takes the form
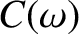 |
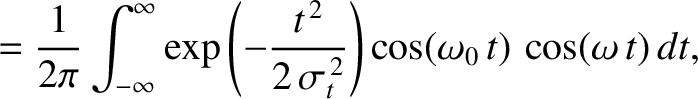 |
|
![$\displaystyle =\frac{1}{4\pi}\int_{-\infty}^\infty \exp\left(-\frac{t^{\,2}}{2\...
...ight)
\left\{\cos[(\omega-\omega_0)\,t] + \cos[(\omega+\omega_0)\,t]\right\}dt.$](img2487.png) |
(8.69) |
![$\displaystyle C(\omega>0) = \frac{1}{2\,(2\pi\,\sigma_\omega^{\,2})^{1/2}}\,\exp\left[-\frac{(\omega-\omega_0)^{\,2}}{2\,\sigma_\omega^{\,2}}\right],$](img2488.png) |
(8.70) |
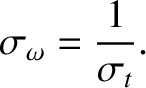 |
(8.71) |
 -space that is centered on the carrier frequency,
-space that is centered on the carrier frequency,  , and
is of characteristic width
, and
is of characteristic width
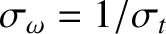 . Thus, the bandwidth of
the signal is of order
. Thus, the bandwidth of
the signal is of order
 . The shorter the signal duration,
the higher the bandwidth. This is a general rule. A signal of full width at half maximum temporal duration
. The shorter the signal duration,
the higher the bandwidth. This is a general rule. A signal of full width at half maximum temporal duration
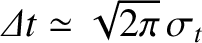 generally has a Fourier transform of full width at half maximum bandwidth
generally has a Fourier transform of full width at half maximum bandwidth
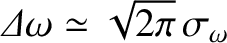 , so that
, so that
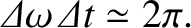 |
(8.72) |
 |
(8.73) |
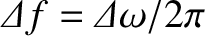 is the bandwidth in hertz.
The previous result is known as the bandwidth theorem. The duration
of a digital bit is closely related to the maximum rate at which information
can be transmitted by a digital signal. Because the individual bits cannot
overlap in time, the maximum number of bits per second that can be transmitted
by a digital signal is of order
is the bandwidth in hertz.
The previous result is known as the bandwidth theorem. The duration
of a digital bit is closely related to the maximum rate at which information
can be transmitted by a digital signal. Because the individual bits cannot
overlap in time, the maximum number of bits per second that can be transmitted
by a digital signal is of order
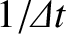 . In other words, it is of order the bandwidth of the signal.
Thus, digital signals that transmit information at a rapid rate require large bandwidths, and, consequently
occupy a wide range of frequency space.
. In other words, it is of order the bandwidth of the signal.
Thus, digital signals that transmit information at a rapid rate require large bandwidths, and, consequently
occupy a wide range of frequency space.
An old-fashioned black and white TV screen consists of a rectangular grid
of black and white spots scanned by an electron beam that can be switched on or off rapidly.
A given spot is “white” if the phosphorescent TV
screen was recently (i.e., within about  th of a second) struck by the
energized electron beam at that location. The spot separation is about
th of a second) struck by the
energized electron beam at that location. The spot separation is about 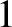 mm. A typical
screen is
mm. A typical
screen is
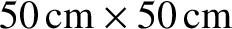 , and thus has 500 lines with
500 spots per line, or
, and thus has 500 lines with
500 spots per line, or
 spots. Each spot is renewed every
spots. Each spot is renewed every 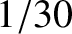 th of
a second. (Every other horizontal line is skipped during a given traversal of the
electron beam over the screen. The skipped lines are renewed on the next
traversal. This technique is known as interlacing. Consequently, a given region of the screen, that includes many horizontal lines,
has a flicker rate of 60 Hz.) Thus, the rate at which the instructions “turn on" and
“turn off” must be sent to the electron beam is
th of
a second. (Every other horizontal line is skipped during a given traversal of the
electron beam over the screen. The skipped lines are renewed on the next
traversal. This technique is known as interlacing. Consequently, a given region of the screen, that includes many horizontal lines,
has a flicker rate of 60 Hz.) Thus, the rate at which the instructions “turn on" and
“turn off” must be sent to the electron beam is
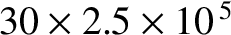 or
or
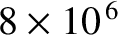 times a second. The transmitted TV signal must therefore
have about
times a second. The transmitted TV signal must therefore
have about 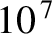 on-off instruction blips per second. If temporal overlap is to be avoided, each blip can be no
longer than
on-off instruction blips per second. If temporal overlap is to be avoided, each blip can be no
longer than
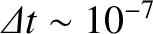 seconds in duration.
Thus, the required bandwidth is
seconds in duration.
Thus, the required bandwidth is
 . The carrier wave frequencies used for conventional broadcast TV lie in the
so-called VHF band, and range
from about 55 to 210 MHz. Our previous discussion of AM radio might lead us
to think that the 10 MHz bandwidth represents the combined extents of an upper and a lower
sideband of modulation frequencies. In practice, the carrier wave and one
of the sidebands are suppressed. That is, they are filtered out, and never applied
to the antenna. However, they are regenerated in the receiver from the information
contained in the single sideband that is broadcast. This technique, which
is called single sideband transmission, halves the bandwidth
requirement to about
. The carrier wave frequencies used for conventional broadcast TV lie in the
so-called VHF band, and range
from about 55 to 210 MHz. Our previous discussion of AM radio might lead us
to think that the 10 MHz bandwidth represents the combined extents of an upper and a lower
sideband of modulation frequencies. In practice, the carrier wave and one
of the sidebands are suppressed. That is, they are filtered out, and never applied
to the antenna. However, they are regenerated in the receiver from the information
contained in the single sideband that is broadcast. This technique, which
is called single sideband transmission, halves the bandwidth
requirement to about
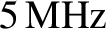 . (Incidentally, the lower sideband carries the same
information as the upper one, and thus can be used to completely regenerate the upper sideband, and vice versa.) Thus, between
. (Incidentally, the lower sideband carries the same
information as the upper one, and thus can be used to completely regenerate the upper sideband, and vice versa.) Thus, between 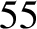 and
and
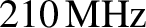 there is room for about 30 TV channels, each using a 5 MHz bandwidth. (Actually,
there are far fewer TV channels than this in the VHF band, because part of this
band is reserved for FM radio, air traffic control, air navigation beacons, marine communications, etc.)
there is room for about 30 TV channels, each using a 5 MHz bandwidth. (Actually,
there are far fewer TV channels than this in the VHF band, because part of this
band is reserved for FM radio, air traffic control, air navigation beacons, marine communications, etc.)