Electromagnetic Waves
Consider a plane electromagnetic wave propagating through a vacuum in the  -direction.
Incidentally, electromagnetic waves are the only
commonly-occurring waves that do not require a medium through which to
propagate.
Suppose that the wave is linearly polarized in the
-direction.
Incidentally, electromagnetic waves are the only
commonly-occurring waves that do not require a medium through which to
propagate.
Suppose that the wave is linearly polarized in the  -direction; that is, its electric
component oscillates in the
-direction; that is, its electric
component oscillates in the  -direction. It follows that the magnetic
component of the wave oscillates in the
-direction. It follows that the magnetic
component of the wave oscillates in the  -direction (Fitzpatrick 2008). According to standard electromagnetic theory (see Appendix C), the wave is
described by the following pair of coupled partial differential equations:
where
-direction (Fitzpatrick 2008). According to standard electromagnetic theory (see Appendix C), the wave is
described by the following pair of coupled partial differential equations:
where  is the electric field-strength, and
is the electric field-strength, and 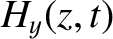 is the
magnetic intensity (i.e., the magnetic field-strength divided by
is the
magnetic intensity (i.e., the magnetic field-strength divided by
 ). Observe that Equations (6.116) and (6.117), which govern
the propagation of electromagnetic waves through a vacuum, are analogous
to Equations (6.53) and (6.54), which govern the propagation of
electromagnetic signals down a transmission line. In particular,
). Observe that Equations (6.116) and (6.117), which govern
the propagation of electromagnetic waves through a vacuum, are analogous
to Equations (6.53) and (6.54), which govern the propagation of
electromagnetic signals down a transmission line. In particular, 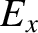 has units of
voltage over length,
has units of
voltage over length, 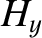 has units of current over length,
has units of current over length,
 has
units of capacitance per unit length, and
has
units of capacitance per unit length, and  has units of
inductance per unit length.
has units of
inductance per unit length.
Equations (6.116) and (6.117) can be combined to give
It follows that the electric and the magnetic components of an electromagnetic wave
propagating through a vacuum both separately satisfy
a wave equation of the form (6.1). Furthermore, the phase velocity of the
wave is the velocity of light in vacuum,
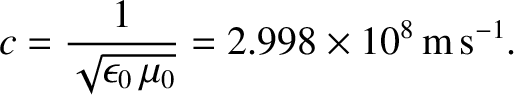 |
(6.120) |
Let us search for a traveling wave solution of Equations (6.116) and (6.117), propagating in the
positive  -direction, whose electric component has the form
-direction, whose electric component has the form
 |
(6.121) |
This is a valid solution provided that
 |
(6.122) |
According to
Equation (6.117), the magnetic component of the wave is written
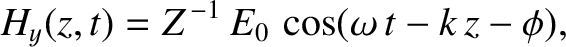 |
(6.123) |
where
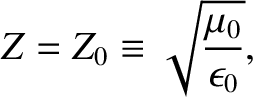 |
(6.124) |
and 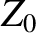 is the impedance of free space. [See Equation (6.74).]
Thus, the electric and magnetic components of an electromagnetic wave propagating through a vacuum are mutually perpendicular,
and also perpendicular to the direction of propagation. Moreover, the two components
oscillate in phase (i.e., they have simultaneous maxima and zeros), and
the amplitude of the magnetic component is that of the electric component
divided by the impedance of free space.
is the impedance of free space. [See Equation (6.74).]
Thus, the electric and magnetic components of an electromagnetic wave propagating through a vacuum are mutually perpendicular,
and also perpendicular to the direction of propagation. Moreover, the two components
oscillate in phase (i.e., they have simultaneous maxima and zeros), and
the amplitude of the magnetic component is that of the electric component
divided by the impedance of free space.
Multiplying Equation (6.116) by
 , Equation (6.117)
by
, Equation (6.117)
by
 , and adding the two resulting expressions, we obtain the
energy conservation equation
, and adding the two resulting expressions, we obtain the
energy conservation equation
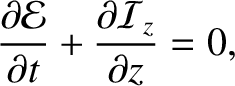 |
(6.125) |
where
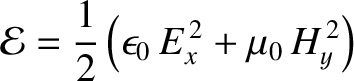 |
(6.126) |
is the energy density (i.e., energy per unit volume) of the wave (Fitzpatrick 2008), whereas
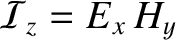 |
(6.127) |
is the energy flux (i.e., power per unit area) in the positive  -direction. (See Appendix C.) The mean energy flux associated with the
-direction. (See Appendix C.) The mean energy flux associated with the  -directed electromagnetic wave specified
in Equations (6.121) and (6.123) is thus
-directed electromagnetic wave specified
in Equations (6.121) and (6.123) is thus
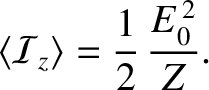 |
(6.128) |
For a similar wave propagating in the negative  -direction, it can be
demonstrated that
and
-direction, it can be
demonstrated that
and
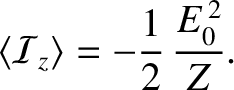 |
(6.131) |
Consider a plane electromagnetic wave, linearly polarized in the  -direction, that
propagates in the
-direction, that
propagates in the  -direction through a transparent dielectric medium, such as glass or water. As is well-known (Fitzpatrick 2008), the electric component of the wave causes the neutral molecules making
up the medium to polarize; that is, it causes a small separation to develop between the mean positions of the positively
and negatively charged constituents of the molecules (i.e., the atomic nuclei and the
orbiting electrons). [Incidentally, it can be
shown that the magnetic component of the wave has a negligible influence on the
molecules, provided the wave amplitude is sufficiently small that the wave electric
field does not cause the electrons and nuclei to move with relativistic velocities (ibid.).] If the mean position of the positively charged
constituents of a given molecule, of net charge
-direction through a transparent dielectric medium, such as glass or water. As is well-known (Fitzpatrick 2008), the electric component of the wave causes the neutral molecules making
up the medium to polarize; that is, it causes a small separation to develop between the mean positions of the positively
and negatively charged constituents of the molecules (i.e., the atomic nuclei and the
orbiting electrons). [Incidentally, it can be
shown that the magnetic component of the wave has a negligible influence on the
molecules, provided the wave amplitude is sufficiently small that the wave electric
field does not cause the electrons and nuclei to move with relativistic velocities (ibid.).] If the mean position of the positively charged
constituents of a given molecule, of net charge 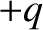 , develops a vector displacement
, develops a vector displacement
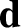 with respect to the mean position of the negatively charged constituents, of net charge
with respect to the mean position of the negatively charged constituents, of net charge 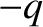 , in response to a wave electric field
, in response to a wave electric field  , then the
associated electric dipole moment is
, then the
associated electric dipole moment is
 , where
, where
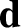 is generally parallel to
is generally parallel to  (ibid.). Furthermore, if there are
(ibid.). Furthermore, if there are  such molecules per unit volume then the electric dipole moment per unit volume
is written
such molecules per unit volume then the electric dipole moment per unit volume
is written
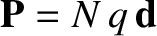 . In a linear, isotropic, dielectric medium (ibid.),
. In a linear, isotropic, dielectric medium (ibid.),
 |
(6.132) |
where
 is a dimensionless quantity, known as the relative dielectric
constant, that is a property of the medium in question. In the presence of
a dielectric medium, Equations (6.116) and (6.117) generalize to give
(See Appendix C.)
When combined with Equation (6.132), these expressions yield
It can be seen that the previous equations are just like the corresponding vacuum equations,
(6.116) and (6.117), except that
is a dimensionless quantity, known as the relative dielectric
constant, that is a property of the medium in question. In the presence of
a dielectric medium, Equations (6.116) and (6.117) generalize to give
(See Appendix C.)
When combined with Equation (6.132), these expressions yield
It can be seen that the previous equations are just like the corresponding vacuum equations,
(6.116) and (6.117), except that
 has been replaced by
has been replaced by
 . It immediately follows that the phase velocity of an
electromagnetic wave propagating through a dielectric medium is
. It immediately follows that the phase velocity of an
electromagnetic wave propagating through a dielectric medium is
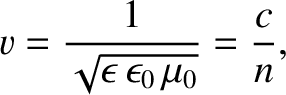 |
(6.137) |
where
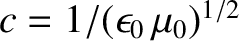 is the velocity of light in vacuum, and
the dimensionless quantity
is the velocity of light in vacuum, and
the dimensionless quantity
 |
(6.138) |
is known as the refractive index of the medium. Thus, an electromagnetic
wave propagating through a transparent dielectric medium does so at a
phase velocity that is less than the velocity of light in vacuum by a
factor  (where
(where 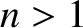 ). The dispersion relation of the wave is thus
). The dispersion relation of the wave is thus
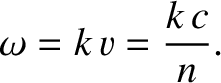 |
(6.139) |
Furthermore, the impedance of a transparent dielectric medium becomes
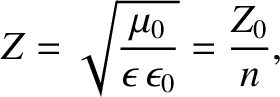 |
(6.140) |
where 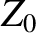 is the impedance of free space.
is the impedance of free space.
Incidentally, the signal that travels down a transmission line is a form of guided electromagnetic wave. It follows
that if the space between the two conductors that constitute the line is filled with dielectric material of
relative dielectric constant 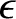 then the signal propagates down the line at the
reduced phase velocity
then the signal propagates down the line at the
reduced phase velocity
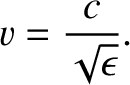 |
(6.141) |
This occurs because the dielectric material
increases the capacitance per unit length of the line by a factor 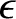 , but leaves the
inductance per unit length unchanged. (See Section 6.6.) For the same reason, the presence of the dielectric
material decreases the impedance of the line by a factor
, but leaves the
inductance per unit length unchanged. (See Section 6.6.) For the same reason, the presence of the dielectric
material decreases the impedance of the line by a factor
 . Hence, the impedance of a
dielectric filled co-axial cable is [cf., Equation (6.78)]
. Hence, the impedance of a
dielectric filled co-axial cable is [cf., Equation (6.78)]
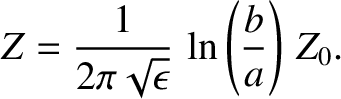 |
(6.142) |
Here, 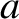 and
and  are the radii of the inner and outer conductors, respectively.
are the radii of the inner and outer conductors, respectively.
Suppose that the plane 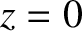 forms the interface between two transparent dielectric
media of refractive indices
forms the interface between two transparent dielectric
media of refractive indices 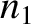 and
and 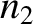 . Let the first medium occupy the
region
. Let the first medium occupy the
region 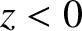 , and the second the region
, and the second the region 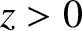 . Suppose that a plane electromagnetic
wave, linearly polarized in the
. Suppose that a plane electromagnetic
wave, linearly polarized in the  -direction, and propagating in the positive
-direction, and propagating in the positive  -direction, is launched toward the interface
from a wave source of angular frequency
-direction, is launched toward the interface
from a wave source of angular frequency  situated at
situated at 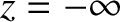 . We expect the
wave incident on the interface to be partly reflected, and partly transmitted.
The wave electric and magnetic fields in the region
. We expect the
wave incident on the interface to be partly reflected, and partly transmitted.
The wave electric and magnetic fields in the region 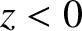 are written
are written
where 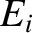 is the amplitude of (the electric component of) the incident wave,
is the amplitude of (the electric component of) the incident wave, 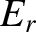 the amplitude of the reflected wave,
the amplitude of the reflected wave,
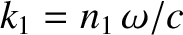 , and
, and
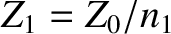 .
The wave electric and magnetic fields in the region
.
The wave electric and magnetic fields in the region 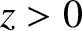 take the form
where
take the form
where 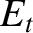 is the amplitude of the transmitted wave,
is the amplitude of the transmitted wave,
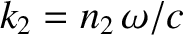 , and
, and
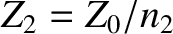 .
According to standard electromagnetic theory (see Appendix C), the appropriate matching conditions at the
interface (
.
According to standard electromagnetic theory (see Appendix C), the appropriate matching conditions at the
interface (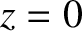 ) are that
) are that 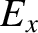 and
and 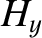 are both continuous. Thus,
continuity of
are both continuous. Thus,
continuity of 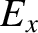 yields
yields
 |
(6.147) |
whereas continuity of 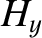 gives
gives
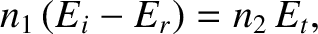 |
(6.148) |
because
 .
It follows that
The coefficient of reflection,
.
It follows that
The coefficient of reflection,  , is defined as the ratio of the reflected to the incident energy
flux, so that
, is defined as the ratio of the reflected to the incident energy
flux, so that
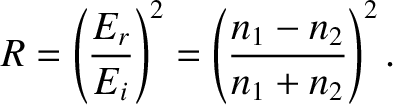 |
(6.151) |
Likewise, the coefficient of transmission,  , is the ratio of the
transmitted to the incident energy flux, so that
, is the ratio of the
transmitted to the incident energy flux, so that
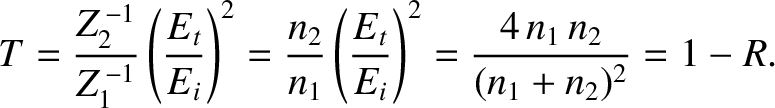 |
(6.152) |
It can be seen, first of all, that if  then
then  and
and  .
In other words, if the two media have the same indices of refraction then
there is no reflection at the interface between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
.
In other words, if the two media have the same indices of refraction then
there is no reflection at the interface between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
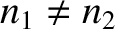 then there is always some reflection at the interface. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between
then there is always some reflection at the interface. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between 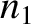 and
and 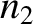 . This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
on an air/glass interface is reflected, as a consequence of the different refractive indices
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass interface.
. This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
on an air/glass interface is reflected, as a consequence of the different refractive indices
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass interface.
According to Equation (6.149),  when
when 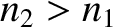 .
The negative sign indicates a
.
The negative sign indicates a 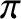 radian phase shift of the (electric component of the) reflected wave, with
respect to the incident wave. We conclude that there is a
radian phase shift of the (electric component of the) reflected wave, with
respect to the incident wave. We conclude that there is a 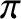 radian phase shift of the reflected wave, relative to the incident wave, on reflection from an
interface with a
medium of greater refractive index. Conversely, there is zero
phase shift
on reflection from an interface with a medium of lesser refractive index. (This effect is important in thin-film interference. See Section 10.5.)
radian phase shift of the reflected wave, relative to the incident wave, on reflection from an
interface with a
medium of greater refractive index. Conversely, there is zero
phase shift
on reflection from an interface with a medium of lesser refractive index. (This effect is important in thin-film interference. See Section 10.5.)
Equations (6.149)–(6.152) are analogous to Equations (6.87)–(6.90), with the inverse of the refractive index playing the role of
impedance. This suggests, by analogy with earlier analysis, that we
can prevent reflection of an electromagnetic wave normally incident at an interface between two
transparent dielectric media of different refractive indices by separating the media in question
by a thin transparent layer whose thickness is one quarter of a wavelength, and whose
refractive index is the geometric mean of the refractive indices of the two
media. This is the physical principle behind the non-reflective lens coatings used
in high-quality optical instruments. (See Exercise 15.)
 -direction.
Incidentally, electromagnetic waves are the only
commonly-occurring waves that do not require a medium through which to
propagate.
Suppose that the wave is linearly polarized in the
-direction.
Incidentally, electromagnetic waves are the only
commonly-occurring waves that do not require a medium through which to
propagate.
Suppose that the wave is linearly polarized in the  -direction; that is, its electric
component oscillates in the
-direction; that is, its electric
component oscillates in the  -direction. It follows that the magnetic
component of the wave oscillates in the
-direction. It follows that the magnetic
component of the wave oscillates in the  -direction (Fitzpatrick 2008). According to standard electromagnetic theory (see Appendix C), the wave is
described by the following pair of coupled partial differential equations:
where
-direction (Fitzpatrick 2008). According to standard electromagnetic theory (see Appendix C), the wave is
described by the following pair of coupled partial differential equations:
where  is the electric field-strength, and
is the electric field-strength, and 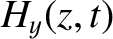 is the
magnetic intensity (i.e., the magnetic field-strength divided by
is the
magnetic intensity (i.e., the magnetic field-strength divided by
 ). Observe that Equations (6.116) and (6.117), which govern
the propagation of electromagnetic waves through a vacuum, are analogous
to Equations (6.53) and (6.54), which govern the propagation of
electromagnetic signals down a transmission line. In particular,
). Observe that Equations (6.116) and (6.117), which govern
the propagation of electromagnetic waves through a vacuum, are analogous
to Equations (6.53) and (6.54), which govern the propagation of
electromagnetic signals down a transmission line. In particular, 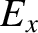 has units of
voltage over length,
has units of
voltage over length, 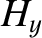 has units of current over length,
has units of current over length,
 has
units of capacitance per unit length, and
has
units of capacitance per unit length, and  has units of
inductance per unit length.
has units of
inductance per unit length.

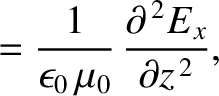
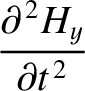

 -direction, whose electric component has the form
-direction, whose electric component has the form

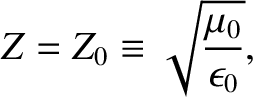
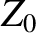 is the impedance of free space. [See Equation (6.74).]
Thus, the electric and magnetic components of an electromagnetic wave propagating through a vacuum are mutually perpendicular,
and also perpendicular to the direction of propagation. Moreover, the two components
oscillate in phase (i.e., they have simultaneous maxima and zeros), and
the amplitude of the magnetic component is that of the electric component
divided by the impedance of free space.
is the impedance of free space. [See Equation (6.74).]
Thus, the electric and magnetic components of an electromagnetic wave propagating through a vacuum are mutually perpendicular,
and also perpendicular to the direction of propagation. Moreover, the two components
oscillate in phase (i.e., they have simultaneous maxima and zeros), and
the amplitude of the magnetic component is that of the electric component
divided by the impedance of free space.
 , Equation (6.117)
by
, Equation (6.117)
by
 , and adding the two resulting expressions, we obtain the
energy conservation equation
, and adding the two resulting expressions, we obtain the
energy conservation equation
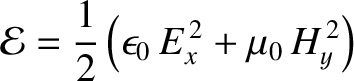
 -direction. (See Appendix C.) The mean energy flux associated with the
-direction. (See Appendix C.) The mean energy flux associated with the  -directed electromagnetic wave specified
in Equations (6.121) and (6.123) is thus
For a similar wave propagating in the negative
-directed electromagnetic wave specified
in Equations (6.121) and (6.123) is thus
For a similar wave propagating in the negative  -direction, it can be
demonstrated that
-direction, it can be
demonstrated that



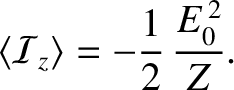
 -direction, that
propagates in the
-direction, that
propagates in the  -direction through a transparent dielectric medium, such as glass or water. As is well-known (Fitzpatrick 2008), the electric component of the wave causes the neutral molecules making
up the medium to polarize; that is, it causes a small separation to develop between the mean positions of the positively
and negatively charged constituents of the molecules (i.e., the atomic nuclei and the
orbiting electrons). [Incidentally, it can be
shown that the magnetic component of the wave has a negligible influence on the
molecules, provided the wave amplitude is sufficiently small that the wave electric
field does not cause the electrons and nuclei to move with relativistic velocities (ibid.).] If the mean position of the positively charged
constituents of a given molecule, of net charge
-direction through a transparent dielectric medium, such as glass or water. As is well-known (Fitzpatrick 2008), the electric component of the wave causes the neutral molecules making
up the medium to polarize; that is, it causes a small separation to develop between the mean positions of the positively
and negatively charged constituents of the molecules (i.e., the atomic nuclei and the
orbiting electrons). [Incidentally, it can be
shown that the magnetic component of the wave has a negligible influence on the
molecules, provided the wave amplitude is sufficiently small that the wave electric
field does not cause the electrons and nuclei to move with relativistic velocities (ibid.).] If the mean position of the positively charged
constituents of a given molecule, of net charge 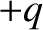 , develops a vector displacement
, develops a vector displacement
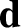 with respect to the mean position of the negatively charged constituents, of net charge
with respect to the mean position of the negatively charged constituents, of net charge 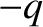 , in response to a wave electric field
, in response to a wave electric field  , then the
associated electric dipole moment is
, then the
associated electric dipole moment is
 , where
, where
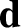 is generally parallel to
is generally parallel to  (ibid.). Furthermore, if there are
(ibid.). Furthermore, if there are  such molecules per unit volume then the electric dipole moment per unit volume
is written
such molecules per unit volume then the electric dipole moment per unit volume
is written
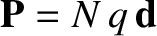 . In a linear, isotropic, dielectric medium (ibid.),
. In a linear, isotropic, dielectric medium (ibid.),
 is a dimensionless quantity, known as the relative dielectric
constant, that is a property of the medium in question. In the presence of
a dielectric medium, Equations (6.116) and (6.117) generalize to give
is a dimensionless quantity, known as the relative dielectric
constant, that is a property of the medium in question. In the presence of
a dielectric medium, Equations (6.116) and (6.117) generalize to give
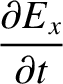
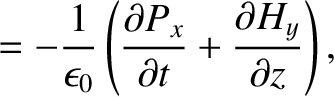
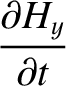
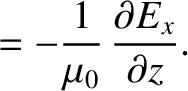
 has been replaced by
has been replaced by
 . It immediately follows that the phase velocity of an
electromagnetic wave propagating through a dielectric medium is
. It immediately follows that the phase velocity of an
electromagnetic wave propagating through a dielectric medium is
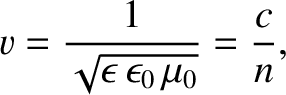
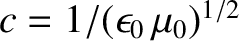 is the velocity of light in vacuum, and
the dimensionless quantity
is the velocity of light in vacuum, and
the dimensionless quantity

 (where
(where 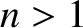 ). The dispersion relation of the wave is thus
). The dispersion relation of the wave is thus
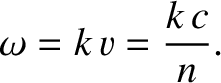
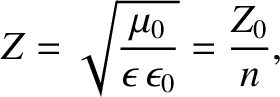
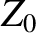 is the impedance of free space.
is the impedance of free space.
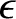 then the signal propagates down the line at the
reduced phase velocity
then the signal propagates down the line at the
reduced phase velocity
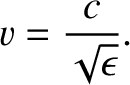
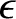 , but leaves the
inductance per unit length unchanged. (See Section 6.6.) For the same reason, the presence of the dielectric
material decreases the impedance of the line by a factor
, but leaves the
inductance per unit length unchanged. (See Section 6.6.) For the same reason, the presence of the dielectric
material decreases the impedance of the line by a factor
 . Hence, the impedance of a
dielectric filled co-axial cable is [cf., Equation (6.78)]
. Hence, the impedance of a
dielectric filled co-axial cable is [cf., Equation (6.78)]
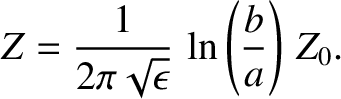
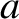 and
and  are the radii of the inner and outer conductors, respectively.
are the radii of the inner and outer conductors, respectively.
 forms the interface between two transparent dielectric
media of refractive indices
forms the interface between two transparent dielectric
media of refractive indices 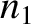 and
and 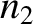 . Let the first medium occupy the
region
. Let the first medium occupy the
region 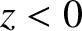 , and the second the region
, and the second the region 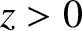 . Suppose that a plane electromagnetic
wave, linearly polarized in the
. Suppose that a plane electromagnetic
wave, linearly polarized in the  -direction, and propagating in the positive
-direction, and propagating in the positive  -direction, is launched toward the interface
from a wave source of angular frequency
-direction, is launched toward the interface
from a wave source of angular frequency  situated at
situated at 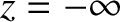 . We expect the
wave incident on the interface to be partly reflected, and partly transmitted.
The wave electric and magnetic fields in the region
. We expect the
wave incident on the interface to be partly reflected, and partly transmitted.
The wave electric and magnetic fields in the region 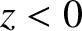 are written
are written

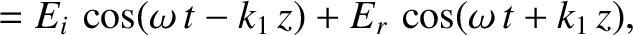
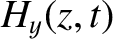

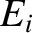 is the amplitude of (the electric component of) the incident wave,
is the amplitude of (the electric component of) the incident wave, 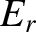 the amplitude of the reflected wave,
the amplitude of the reflected wave,
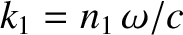 , and
, and
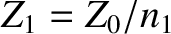 .
The wave electric and magnetic fields in the region
.
The wave electric and magnetic fields in the region 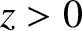 take the form
take the form

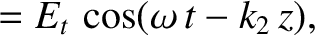
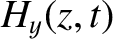
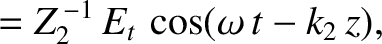
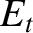 is the amplitude of the transmitted wave,
is the amplitude of the transmitted wave,
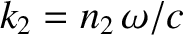 , and
, and
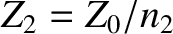 .
According to standard electromagnetic theory (see Appendix C), the appropriate matching conditions at the
interface (
.
According to standard electromagnetic theory (see Appendix C), the appropriate matching conditions at the
interface (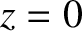 ) are that
) are that 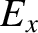 and
and 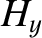 are both continuous. Thus,
continuity of
are both continuous. Thus,
continuity of 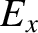 yields
yields

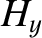 gives
gives
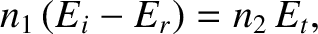
 .
It follows that
.
It follows that
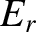
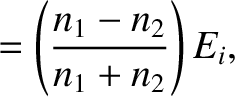
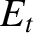
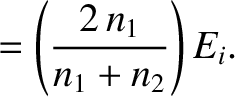
 , is defined as the ratio of the reflected to the incident energy
flux, so that
Likewise, the coefficient of transmission,
, is defined as the ratio of the reflected to the incident energy
flux, so that
Likewise, the coefficient of transmission,  , is the ratio of the
transmitted to the incident energy flux, so that
, is the ratio of the
transmitted to the incident energy flux, so that
 then
then  and
and  .
In other words, if the two media have the same indices of refraction then
there is no reflection at the interface between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
.
In other words, if the two media have the same indices of refraction then
there is no reflection at the interface between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
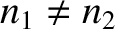 then there is always some reflection at the interface. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between
then there is always some reflection at the interface. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between 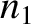 and
and 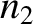 . This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
on an air/glass interface is reflected, as a consequence of the different refractive indices
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass interface.
. This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
on an air/glass interface is reflected, as a consequence of the different refractive indices
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass interface.
 when
when 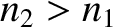 .
The negative sign indicates a
.
The negative sign indicates a 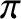 radian phase shift of the (electric component of the) reflected wave, with
respect to the incident wave. We conclude that there is a
radian phase shift of the (electric component of the) reflected wave, with
respect to the incident wave. We conclude that there is a 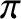 radian phase shift of the reflected wave, relative to the incident wave, on reflection from an
interface with a
medium of greater refractive index. Conversely, there is zero
phase shift
on reflection from an interface with a medium of lesser refractive index. (This effect is important in thin-film interference. See Section 10.5.)
radian phase shift of the reflected wave, relative to the incident wave, on reflection from an
interface with a
medium of greater refractive index. Conversely, there is zero
phase shift
on reflection from an interface with a medium of lesser refractive index. (This effect is important in thin-film interference. See Section 10.5.)