Next: Physical Constants Up: Wave Mechanics Previous: White-Dwarf Star Contents
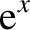 |
 |
|
 |
 |
|
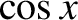 |
 |
 ,
to prove Euler's theorem,
,
to prove Euler's theorem,

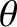 is real.
is real.

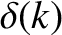 is a Dirac delta function.
Use this result to prove Fourier's theorem; that is, if
is a Dirac delta function.
Use this result to prove Fourier's theorem; that is, if
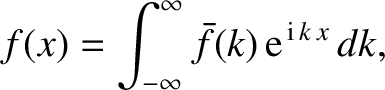
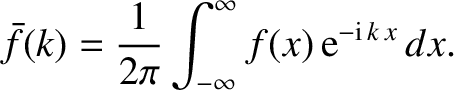
 . How many photons are emitted per second
by a laser with a power of
. How many photons are emitted per second
by a laser with a power of
 ? What force does such a laser exert on a body that completely absorbs
its radiation?
? What force does such a laser exert on a body that completely absorbs
its radiation?
 . Calculate the
frequency (in hertz), wavelength, and wavenumber of the electromagnetic radiation that will just ionize the atom.
. Calculate the
frequency (in hertz), wavelength, and wavenumber of the electromagnetic radiation that will just ionize the atom.
 for radiation of wavelength
for radiation of wavelength
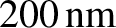 ,
and
,
and
 for radiation of wavelength
for radiation of wavelength
 . Use this data to calculate Planck's
constant (divided by
. Use this data to calculate Planck's
constant (divided by 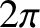 ) and the work function of aluminum. [Adapted from Gasiorowicz 1996.]
) and the work function of aluminum. [Adapted from Gasiorowicz 1996.]
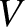 is given by
is given by

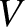 is measured in volts. [From Pain 1999.]
is measured in volts. [From Pain 1999.]
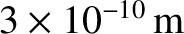 demonstrate that an accelerating
voltage of about
demonstrate that an accelerating
voltage of about
 would be required to produce a useful electron diffraction pattern from the crystal. [Modified from Pain 1999.]
would be required to produce a useful electron diffraction pattern from the crystal. [Modified from Pain 1999.]
 has a wavefunction
has a wavefunction
![$\displaystyle \psi(x,t)= A\,\exp\left[-a\,(m\,x^{\,2}/\hbar+ {\rm i}\,t)\right],
$](img4234.png)
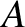 and
and 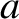 are positive real constants. For what potential
are positive real constants. For what potential  does
does 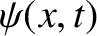 satisfy
Schrödinger's equation?
satisfy
Schrödinger's equation?
 trapped in a one-dimensional square potential well
of width
trapped in a one-dimensional square potential well
of width 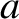 , and infinite depth, returns to its original form after a quantum revival time;
, and infinite depth, returns to its original form after a quantum revival time;
 .
.

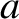 ,
,  ,
, 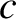 , and
infinite depth, is
, and
infinite depth, is
 . Here,
. Here, 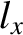 ,
, 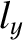 , and
, and
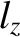 are positive integers. [From Pain 1999.]
are positive integers. [From Pain 1999.]

 , and
, and
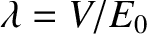 . Hence, demonstrate that for a shallow well (i.e.,
. Hence, demonstrate that for a shallow well (i.e.,
 )
)
 ,
whereas for a deep well (i.e.,
,
whereas for a deep well (i.e.,
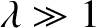 )
)
 (assuming that the particle is in the ground state).
(assuming that the particle is in the ground state).
 penetrating a distance
penetrating a distance  into a classically
forbidden region is proportional to
into a classically
forbidden region is proportional to
 , where
, where

 and
and
 show that
show that
 is approximately equal to
is approximately equal to  for an electron, and
for an electron, and
 for a proton. [Modified from Pain 1999.]
for a proton. [Modified from Pain 1999.]
 and energy
and energy  encounter a
potential step of height
encounter a
potential step of height  ; that is,
; that is,  for
for 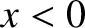 , and
, and
 for
for 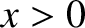 , with the particles incident from
, with the particles incident from  . Show that the fraction
reflected is
. Show that the fraction
reflected is

 and
and
 .
.

 . Demonstrate that the bound-states of a particle of
mass
. Demonstrate that the bound-states of a particle of
mass  and energy
and energy  satisfy
satisfy

 , calculate the Fermi
energy in electron volts, and the velocity of an electron whose kinetic
energy is equal to the Fermi energy.
, calculate the Fermi
energy in electron volts, and the velocity of an electron whose kinetic
energy is equal to the Fermi energy.