Next: Schrödinger's Equation Up: Wave Mechanics Previous: Electron Diffraction Contents
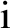 is conventionally used to represent the square-root of minus one; that is, the
solution of
is conventionally used to represent the square-root of minus one; that is, the
solution of
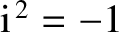 (Riley 1974). A real number,
(Riley 1974). A real number,  (say), can take any value in a continuum of values lying between
(say), can take any value in a continuum of values lying between  and
and 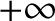 .
On the other hand, an imaginary number takes the general form
.
On the other hand, an imaginary number takes the general form
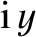 , where
, where  is a real number. It follows that the square of
a real number is a positive real number, whereas the square of an imaginary number is a negative real number. In addition, a general complex number is written
is a real number. It follows that the square of
a real number is a positive real number, whereas the square of an imaginary number is a negative real number. In addition, a general complex number is written
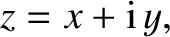 |
(11.6) |
 and
and  are real numbers. In fact,
are real numbers. In fact,  is termed the real part of
is termed the real part of  , and
, and  the imaginary part of
the imaginary part of  . This is written mathematically as
. This is written mathematically as
 and
and
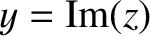 .
Finally, the complex conjugate of
.
Finally, the complex conjugate of  is defined
is defined
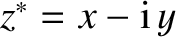 .
.
Just as we
can visualize a real number as a point on an infinite straight line, we can visualize a complex number as
a point in an infinite plane. The coordinates of the point in question are the real and imaginary
parts of the number; that is,
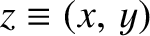 . This idea is illustrated in Figure 11.2.
The distance,
. This idea is illustrated in Figure 11.2.
The distance,
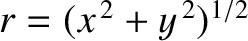 , of the representative point from the origin is termed the modulus
of the corresponding complex number,
, of the representative point from the origin is termed the modulus
of the corresponding complex number,  . This is written mathematically as
. This is written mathematically as
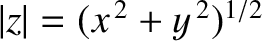 . Incidentally, it follows that
. Incidentally, it follows that
 .
The angle,
.
The angle,
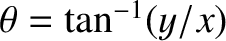 , that the straight line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number,
, that the straight line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number,  . This is written mathematically
as
. This is written mathematically
as
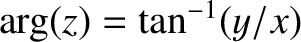 . It follows from standard trigonometry that
. It follows from standard trigonometry that
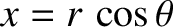 , and
, and
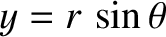 .
Hence,
.
Hence,
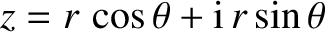 .
.
Complex numbers are often used to represent waves and wavefunctions. All such representations ultimately depend on a fundamental mathematical identity, known as Euler's theorem (see Exercise 2), which takes the form
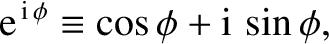 |
(11.7) |
 is a real number (Riley 1974). Incidentally, given that
is a real number (Riley 1974). Incidentally, given that
![$z=r\,\cos\theta + {\rm i}\,r\,\sin\theta= r\,[\cos\theta+{\rm i}\,\sin\theta]$](img3818.png) , where
, where  is a general
complex number,
is a general
complex number, 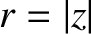 its modulus, and
its modulus, and
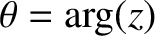 its argument, it follows from Euler's theorem that any
complex number,
its argument, it follows from Euler's theorem that any
complex number,  , can be written
, can be written
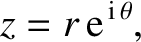 |
(11.8) |
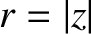 and
and
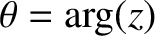 are real numbers.
are real numbers.
A one-dimensional wavefunction takes the general form
where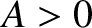 is the wave amplitude,
is the wave amplitude,  the phase angle,
the phase angle,  the wavenumber, and
the wavenumber, and  the angular
frequency. Consider the complex wavefunction
where
the angular
frequency. Consider the complex wavefunction
where 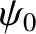 is a complex constant. We can write
is a complex constant. We can write
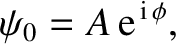 |
(11.11) |
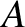 is the modulus, and
is the modulus, and  the argument, of
the argument, of 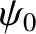 .
Hence, we deduce that
.
Hence, we deduce that
![$\displaystyle {\rm Re}\left[\psi_0\,{\rm e}^{-{\rm i}\,(\omega\,t-k\,x)}\right]...
...phi)}\right]=A\,{\rm Re}\left[{\rm e}^{-{\rm i}\,(\omega\,t-k\,x-\phi)}\right].$](img3824.png) |
(11.12) |
![$\displaystyle {\rm Re}\left[\psi_0\,{\rm e}^{-{\rm i}\,(\omega\,t-k\,x)}\right] =A\,\cos(\omega\,t-k\,x-\phi)=\psi(x,t).$](img3825.png) |
(11.13) |
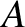 , and the
phase angle,
, and the
phase angle,  , of the wavefunction into a single complex amplitude,
, of the wavefunction into a single complex amplitude, 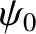 .
.