Next: Representation of Waves via Up: Wave Mechanics Previous: Photoelectric Effect Contents
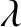 , or, alternatively, the wavenumber,
, or, alternatively, the wavenumber,
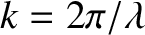 , can be deduced from the spacing
of the maxima in the interference pattern. (See Chapter 10.)
Thomson found that the momentum,
, can be deduced from the spacing
of the maxima in the interference pattern. (See Chapter 10.)
Thomson found that the momentum, 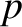 , of an electron is related to its wavenumber,
, of an electron is related to its wavenumber, 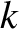 , according to the
following
simple relation:
(Gasiorowicz 1996).
The associated wavelength,
, according to the
following
simple relation:
(Gasiorowicz 1996).
The associated wavelength,
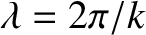 , is known as the de Broglie wavelength, because this relation was first hypothesized by Louis de Broglie in 1926.
In the following, we shall assume that Equation (11.3) is a general result that applies to all particles, not just electrons.
, is known as the de Broglie wavelength, because this relation was first hypothesized by Louis de Broglie in 1926.
In the following, we shall assume that Equation (11.3) is a general result that applies to all particles, not just electrons.
It turns out that wave-particle duality only manifests itself on lengthscales less than, or of order, the de Broglie wavelength (Dirac 1982). Under normal circumstances, this wavelength is fairly small. For instance, the de Broglie wavelength of an electron is
![$\displaystyle \lambda_e = 1.2\times 10^{-9}\,[E({\rm eV})]^{-1/2}\,{\rm m},$](img3794.png) |
(11.4) |
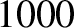 V
acquires an energy of
V
acquires an energy of 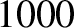 eV, and so on. Electrons in atoms typically have energies in the range
eV, and so on. Electrons in atoms typically have energies in the range 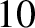 to
to 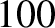 eV.) Moreover, the de Broglie wavelength
of a proton is
eV.) Moreover, the de Broglie wavelength
of a proton is
![$\displaystyle \lambda_p = 2.9\times 10^{-11}\,[E({\rm eV})]^{-1/2}\,{\rm m}.$](img3798.png) |
(11.5) |