Next: Wave Mechanics Up: Wave Optics Previous: Diffraction from Circular Disk Contents
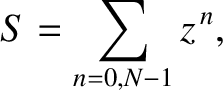
 is a complex number. Demonstrate that
is a complex number. Demonstrate that
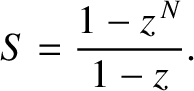
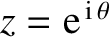 , where
, where 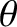 is real. Employing the well-known
identity
is real. Employing the well-known
identity
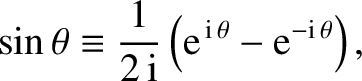
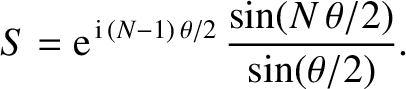
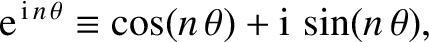
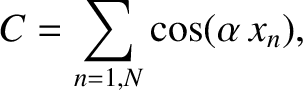
![$\displaystyle x_n = [n-(N+1)/2]\,d,$](img3453.png)
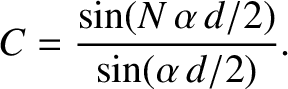
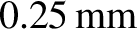 , and monochromatic light of wavelength
, and monochromatic light of wavelength
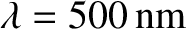 .
Estimate the minimum distance that the projection screen must be placed behind the slits in order to obtain a far-field interference
pattern.
.
Estimate the minimum distance that the projection screen must be placed behind the slits in order to obtain a far-field interference
pattern.
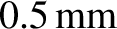 is illuminated at normal incidence by a parallel beam from
a helium-neon laser that emits monochromatic light of wavelength
is illuminated at normal incidence by a parallel beam from
a helium-neon laser that emits monochromatic light of wavelength
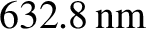 . A projection
screen is located
. A projection
screen is located
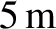 behind the slit. What is the separation of the central interference fringes on the screen? [From Crawford 1968.]
behind the slit. What is the separation of the central interference fringes on the screen? [From Crawford 1968.]
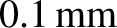 , and the
projection screen is located
, and the
projection screen is located
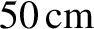 behind the slits. Assuming monochromatic illumination at normal incidence, if the observed separation between neighboring interference
maxima at the center of the projection screen is
behind the slits. Assuming monochromatic illumination at normal incidence, if the observed separation between neighboring interference
maxima at the center of the projection screen is
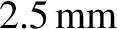 , what is the wavelength of the
light illuminating the slits?
, what is the wavelength of the
light illuminating the slits?
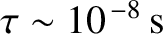 ? In an ordinary gas-discharge source, the
excited atomic states do not decay freely, but instead have an effective lifetime
? In an ordinary gas-discharge source, the
excited atomic states do not decay freely, but instead have an effective lifetime
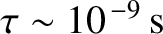 , due to
collisions and Doppler effects. What is the length of the corresponding classical wavetrain? [From Crawford 1968.]
, due to
collisions and Doppler effects. What is the length of the corresponding classical wavetrain? [From Crawford 1968.]
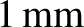 , estimate the
minimum distance it can
be placed in front of a double-slit, of slit separation
, estimate the
minimum distance it can
be placed in front of a double-slit, of slit separation
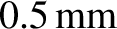 , if the light from the slit is to generate a
clear interference pattern.
, if the light from the slit is to generate a
clear interference pattern.
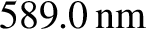 and
and
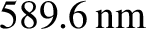 . Demonstrate that a diffraction
grating must have at least 328 lines in order to resolve this doublet at the third spectral order.
. Demonstrate that a diffraction
grating must have at least 328 lines in order to resolve this doublet at the third spectral order.
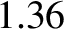 .
Which colors are not seen in the reflected light? Which colors
appear bright in the reflected light? What color does the soap film
appear at normal incidence?
.
Which colors are not seen in the reflected light? Which colors
appear bright in the reflected light? What color does the soap film
appear at normal incidence?
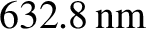 emits a
diffraction-limited beam of initial diameter 2 mm. Estimate how large a light spot
the beam would produce on the surface of the Moon (which is a mean distance
emits a
diffraction-limited beam of initial diameter 2 mm. Estimate how large a light spot
the beam would produce on the surface of the Moon (which is a mean distance
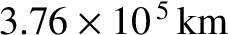 from the surface of the Earth). Neglect any effects of the Earth's atmosphere. [From Hecht and Zajac 1974.]
from the surface of the Earth). Neglect any effects of the Earth's atmosphere. [From Hecht and Zajac 1974.]
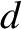 , and the slit width
, and the slit width 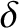 .
Show that the intensity of the far-field interference pattern, assuming normal incidence by monochromatic
light of wavelength
.
Show that the intensity of the far-field interference pattern, assuming normal incidence by monochromatic
light of wavelength 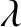 , is
, is
 and
and
 .
.
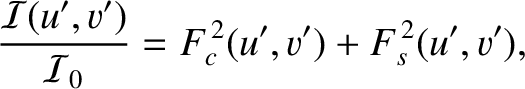
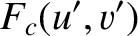 |
![$\displaystyle =\frac{1}{2}\int_{-\infty}^\infty\int_{-\infty}^\infty f(u,v)\,\cos\left[\pi\,(u\,u'+v\,v')\right]\,du\,dv,$](img3746.png) |
|
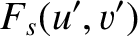 |
![$\displaystyle =\frac{1}{2}\int_{-\infty}^\infty\int_{-\infty}^\infty f(u,v)\,\sin\left[\pi\,(u\,u'+v\,v')\right]\,du\,dv.$](img3748.png) |
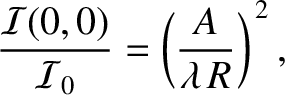
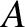 is the area of the aperture,
is the area of the aperture, 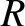 the distance of the projection screen behind the aperture,
and
the distance of the projection screen behind the aperture,
and 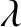 the wavelength.
the wavelength.
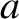 , normally illuminated by monochromatic light of wavelength
, normally illuminated by monochromatic light of wavelength 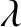 . Let
. Let 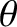 denote the angular
distance from the optic axis (i.e., the line that passes through the center of the aperture, and is perpendicular to the plane of the aperture and the projection screen) on the projection screen.
Demonstrate that the mean energy flux that falls within the region
denote the angular
distance from the optic axis (i.e., the line that passes through the center of the aperture, and is perpendicular to the plane of the aperture and the projection screen) on the projection screen.
Demonstrate that the mean energy flux that falls within the region
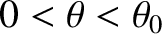 is
is
![$\displaystyle {\cal I}_0\,\pi\,a^{\,2}\left[1-J_0^{\,2}(k\,a\,\theta_0)-J_1^{\,2}(k\,a\,\theta_0)\right],
$](img3751.png)
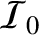 is the intensity of the incident wave, and
is the intensity of the incident wave, and
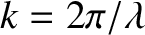 .
[Hint:
.
[Hint:
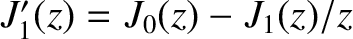 and
and
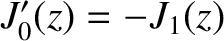 , where
, where 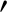 denotes a derivative with respect to
argument.]
Hence, deduce that the total energy flux that illuminates the projection screen is the same
as that predicted by geometric optics. Finally, show that the Airy disk contains approximately
denotes a derivative with respect to
argument.]
Hence, deduce that the total energy flux that illuminates the projection screen is the same
as that predicted by geometric optics. Finally, show that the Airy disk contains approximately 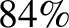 of the total
energy flux.
of the total
energy flux.
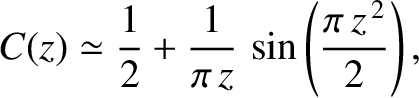 |
|
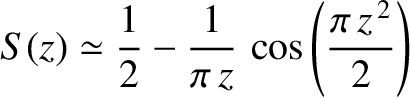 |
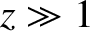 . Use these forms to demonstrate that the intensity of
a diffraction pattern of a semi-infinite opaque plane bounded by a sharp straight edge, which is specified in Equation (10.132), reduces to
. Use these forms to demonstrate that the intensity of
a diffraction pattern of a semi-infinite opaque plane bounded by a sharp straight edge, which is specified in Equation (10.132), reduces to
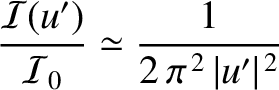
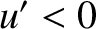 and
and 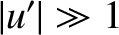 ). This implies that the intensity in the shadow region attenuates
as the inverse-square of the distance from the straight edge.
). This implies that the intensity in the shadow region attenuates
as the inverse-square of the distance from the straight edge.
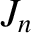 Bessel functions satisfy the recursion relation (Abramowitz and Stegun 1965)
Bessel functions satisfy the recursion relation (Abramowitz and Stegun 1965)
![$\displaystyle \frac{d}{dz}\left[z^{\,n+1}\,J_{n+1}(z)\right]=z^{\,n+1}\,J_n(z),
$](img3763.png)
 is a non-negative integer. By repeatedly integrating by parts, demonstrate that the functions
is a non-negative integer. By repeatedly integrating by parts, demonstrate that the functions
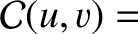 |
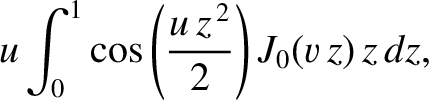 |
|
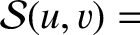 |
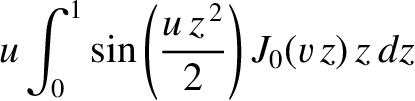 |
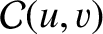 |
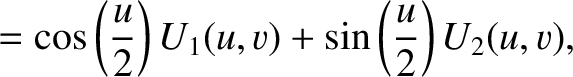 |
|
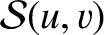 |
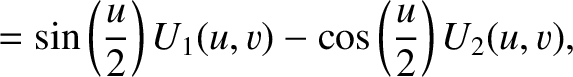 |
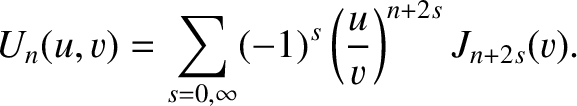
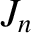 Bessel functions also satisfy the recursion relation (Abramowitz and Stegun 1965)
Bessel functions also satisfy the recursion relation (Abramowitz and Stegun 1965)
![$\displaystyle \frac{d}{dz}\left[z^{-n}\,J_{n}(z)\right]=-z^{-n}\,J_{n+1}(z),
$](img3770.png)
 is a non-negative integer. By repeatedly integrating by parts, demonstrate that
is a non-negative integer. By repeatedly integrating by parts, demonstrate that
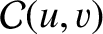 |
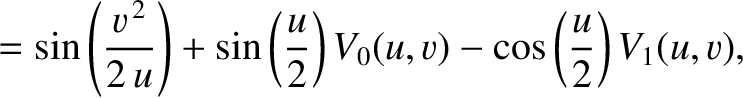 |
|
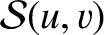 |
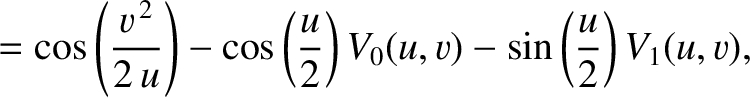 |
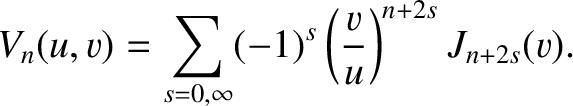
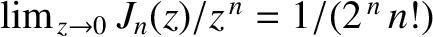 (Abramowitz and Stegun 1965).
(Abramowitz and Stegun 1965).
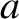 , normally
illuminated by monochromatic light of wavelength
, normally
illuminated by monochromatic light of wavelength 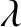 .
.
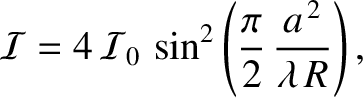
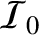 is the intensity of the incident wave, and
is the intensity of the incident wave, and 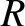 is the distance of the
projection screen behind the aperture. Hence, deduce that if the so-called Fresnel number,
is the distance of the
projection screen behind the aperture. Hence, deduce that if the so-called Fresnel number,
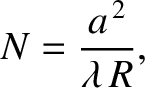
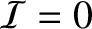 , and if the Fresnel number takes an odd-integer
value then
, and if the Fresnel number takes an odd-integer
value then
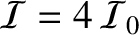 .
.
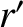 from the optic axis
asymptotes to
from the optic axis
asymptotes to
![$\displaystyle {\cal I}= {\cal I}_0\left[\frac{a}{r'}\,J_1\left(2\pi\,\frac{a\,r'}{\lambda\,R}\right)\right]^{\,2}
$](img3779.png)
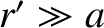 .
.
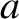 , normally
illuminated by monochromatic light of wavelength
, normally
illuminated by monochromatic light of wavelength 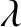 .
.
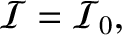
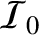 is the intensity of the incident wave.
is the intensity of the incident wave.
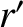 from the optic axis
asymptotes to
from the optic axis
asymptotes to
![$\displaystyle {\cal I}= {\cal I}_0\left[1-\frac{2\,a}{r'}\,J_1\left(2\pi\,\frac...
...r'}{\lambda\,R}\right)\sin\left(\pi\,\frac{r'^{\,2}}{\lambda\,R}\right)\right]
$](img3782.png)
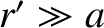 . Here,
. Here,  is the distance of the
projection screen behind the aperture.
is the distance of the
projection screen behind the aperture.