Huygens–Fresnel Principle
Let us again consider a monochromatic plane light wave, propagating in the  -direction, which is normally incident on an opaque
screen that occupies the plane
-direction, which is normally incident on an opaque
screen that occupies the plane 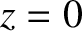 . Suppose that there is an irregularly shaped aperture cut in the screen, and
that the light that passes through this aperture travels to a flat projection screen occupying the plane
. Suppose that there is an irregularly shaped aperture cut in the screen, and
that the light that passes through this aperture travels to a flat projection screen occupying the plane 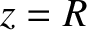 .
Let
.
Let
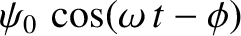 be the electric component of the wave illuminating the opaque screen from behind (i.e., from
be the electric component of the wave illuminating the opaque screen from behind (i.e., from 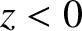 ).
We can determine the diffraction pattern that appears on the projection screen by using a more accurate version of
Huygen's principle known as the Hugyens–Fresnel principle. According to this principle, each
unblocked element of the opaque screen emits a secondary wave of the form (Jackson 1975)
).
We can determine the diffraction pattern that appears on the projection screen by using a more accurate version of
Huygen's principle known as the Hugyens–Fresnel principle. According to this principle, each
unblocked element of the opaque screen emits a secondary wave of the form (Jackson 1975)
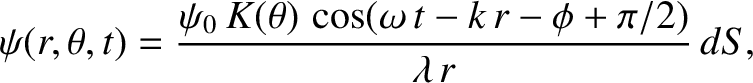 |
(10.88) |
where 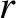 is the distance that the wave has propagated,
is the distance that the wave has propagated, 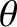 the angle subtended between the
direction of propagation and the direction of incidence (i.e., the
the angle subtended between the
direction of propagation and the direction of incidence (i.e., the  -axis),
-axis), 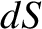 the area of the element, and
the area of the element, and
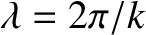 the wavelength. Here,
the wavelength. Here, 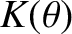 is known as the obliquity factor. Previously (in Section 10.9), we effectively assumed that
is known as the obliquity factor. Previously (in Section 10.9), we effectively assumed that
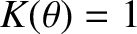 for
for
 , and
, and
 for
for
 . In other words, we assumed that the secondary wave is a half-spherical wave that is emitted isotropically in all forward directions, and
has zero amplitude in all backward directions. In fact, the true obliquity factor is (Jackson 1975)
. In other words, we assumed that the secondary wave is a half-spherical wave that is emitted isotropically in all forward directions, and
has zero amplitude in all backward directions. In fact, the true obliquity factor is (Jackson 1975)
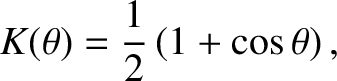 |
(10.89) |
which implies that, although the secondary wave propagates predominately in the forward direction, there is
some backward propagation. According to Equation (10.88), there is a  phase difference between the secondary wave emitted by an element of the aperture, and the light that
illuminates the element from behind. We previously (in Section 10.9) assumed that there was no phase difference.
However, it is easily demonstrated that none of our previous results would be modified had we taken this
phase difference into account.
phase difference between the secondary wave emitted by an element of the aperture, and the light that
illuminates the element from behind. We previously (in Section 10.9) assumed that there was no phase difference.
However, it is easily demonstrated that none of our previous results would be modified had we taken this
phase difference into account.
Let us define a modified aperture function, 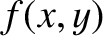 , which is such that
, which is such that 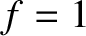 if the
point (
if the
point ( ,
,  , 0) on the opaque screen falls within the aperture, and
, 0) on the opaque screen falls within the aperture, and 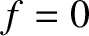 otherwise. It follows
from Equation (10.88) that the wave amplitude at the point (
otherwise. It follows
from Equation (10.88) that the wave amplitude at the point (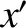 ,
,  ,
,  ) on the projection
screen, which is the resultant of all of the secondary waves that are emitted by the aperture
and travel to this particular point, is given by
) on the projection
screen, which is the resultant of all of the secondary waves that are emitted by the aperture
and travel to this particular point, is given by
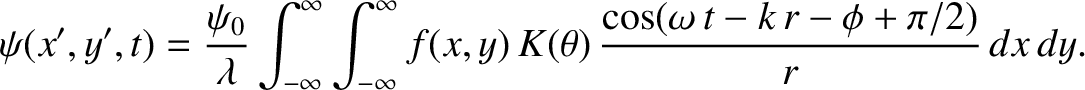 |
(10.90) |
Now,
and
![$\displaystyle \cos\theta \equiv \frac{R}{r} = 1-\frac{(x-x')^{\,2}}{2\,R^{\,2}}...
...-x')^{\,4}}{R^{\,4}}\right]
+{\cal O}\left[\frac{(y-y')^{\,4}}{R^{\,4}}\right].$](img3557.png) |
(10.92) |
Let us assume that
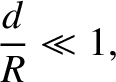 |
(10.93) |
where  is the typical aperture dimension (or, to be more exact, the typical value of
is the typical aperture dimension (or, to be more exact, the typical value of 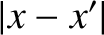 and
and 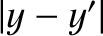 ). In
this limit, Equation (10.90) reduces to
). In
this limit, Equation (10.90) reduces to
![$\displaystyle \psi(x',y',t) \simeq -\frac{\psi_0}{\lambda\,R}\int_{-\infty}^\in...
...ga\,t-k\,R-\phi-\frac{k\,(x-x')^2}{2\,R}-\frac{k\,(y-y')^2}{2\,R}\right]dx\,dy,$](img3561.png) |
(10.94) |
where use has been made of the trigonometric identity
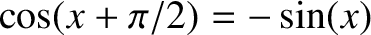 .
The neglect of terms involving
.
The neglect of terms involving
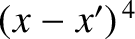 and
and
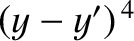 inside the argument of the sine function in the previous equation is
justified provided that
inside the argument of the sine function in the previous equation is
justified provided that
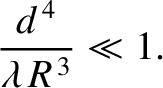 |
(10.95) |
Note that this is a far less stringent criterion than the far-field criterion (see Section 10.2)
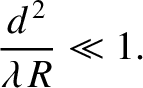 |
(10.96) |
Hence, Equation (10.94) is valid not only in the far-field limit (specified by the previous inequality),
but also in the so-called near-field limit specified by the inequality
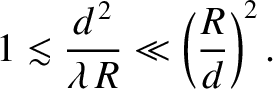 |
(10.97) |
Expression (10.94) is more general than our previous far-field expression, (10.74),
because we have retained terms in the argument of the sine function that are quadratic
in  and
and  , whereas these terms were previously neglected.
Incidentally, far-field diffraction is often referred to as Fraunhofer diffraction, whereas
near-field diffraction is termed Fresnel diffraction.
Note, finally, that because the ordering
, whereas these terms were previously neglected.
Incidentally, far-field diffraction is often referred to as Fraunhofer diffraction, whereas
near-field diffraction is termed Fresnel diffraction.
Note, finally, that because the ordering  implies that
implies that
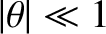 , our previous incorrect assumption for the form of the obliquity factor
makes no difference, because our previous form and the correct form are both characterized by
, our previous incorrect assumption for the form of the obliquity factor
makes no difference, because our previous form and the correct form are both characterized by
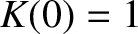 .
.
Let
Thus, 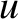 and
and  are dimensionless coordinates that locate a point within the aperture, whereas
are dimensionless coordinates that locate a point within the aperture, whereas
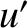 and
and 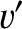 are corresponding coordinates that locate a point on the projection screen.
Equation (10.94) transforms to give
are corresponding coordinates that locate a point on the projection screen.
Equation (10.94) transforms to give
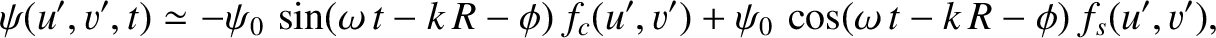 |
(10.102) |
where
Suppose that the aperture is completely transparent, so that  for all
for all 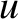 and
and  .
In this case, the two-dimensional integrals in the previous two equations become separable. Making use of some standard trigonometric identities (see Section B.3), we obtain
.
In this case, the two-dimensional integrals in the previous two equations become separable. Making use of some standard trigonometric identities (see Section B.3), we obtain
However, (Abramowitz and Stegun 1965)
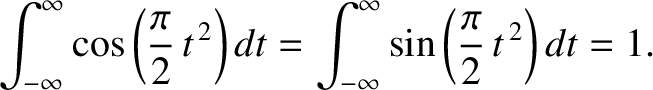 |
(10.107) |
Hence, we deduce that
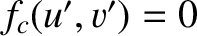 and
and
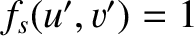 , which, from Equation (10.102), implies that
, which, from Equation (10.102), implies that
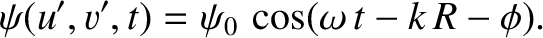 |
(10.108) |
Of course, this is the correct answer; if the aperture is completely transparent (i.e., if 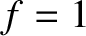 everywhere) then the incident wave,
everywhere) then the incident wave,
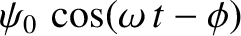 , illuminating the aperture from behind, propagates in the
, illuminating the aperture from behind, propagates in the  -direction without changing amplitude, and acquires a phase shift
-direction without changing amplitude, and acquires a phase shift 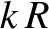 by the time
it reaches the projection screen. The previous result is the ultimate justification for the
Hugyens–Fresnel formula, (10.88).
by the time
it reaches the projection screen. The previous result is the ultimate justification for the
Hugyens–Fresnel formula, (10.88).
The intensity at which a given point on the projection screen is illuminated is (see Section 10.2)
 |
(10.109) |
where
 denotes an average over a wave period.
It follows from Equation (10.102) that
denotes an average over a wave period.
It follows from Equation (10.102) that
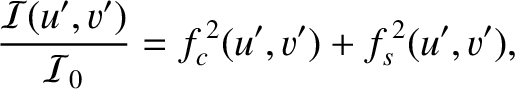 |
(10.110) |
where
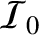 is the illumination intensity when the aperture is completely transparent.
Here, use has been made of the standard results
is the illumination intensity when the aperture is completely transparent.
Here, use has been made of the standard results
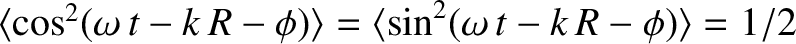 and
and
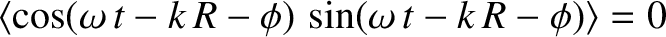 .
.
 -direction, which is normally incident on an opaque
screen that occupies the plane
-direction, which is normally incident on an opaque
screen that occupies the plane 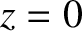 . Suppose that there is an irregularly shaped aperture cut in the screen, and
that the light that passes through this aperture travels to a flat projection screen occupying the plane
. Suppose that there is an irregularly shaped aperture cut in the screen, and
that the light that passes through this aperture travels to a flat projection screen occupying the plane 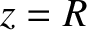 .
Let
.
Let
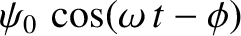 be the electric component of the wave illuminating the opaque screen from behind (i.e., from
be the electric component of the wave illuminating the opaque screen from behind (i.e., from  ).
We can determine the diffraction pattern that appears on the projection screen by using a more accurate version of
Huygen's principle known as the Hugyens–Fresnel principle. According to this principle, each
unblocked element of the opaque screen emits a secondary wave of the form (Jackson 1975)
where
).
We can determine the diffraction pattern that appears on the projection screen by using a more accurate version of
Huygen's principle known as the Hugyens–Fresnel principle. According to this principle, each
unblocked element of the opaque screen emits a secondary wave of the form (Jackson 1975)
where 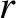 is the distance that the wave has propagated,
is the distance that the wave has propagated, 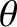 the angle subtended between the
direction of propagation and the direction of incidence (i.e., the
the angle subtended between the
direction of propagation and the direction of incidence (i.e., the  -axis),
-axis), 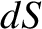 the area of the element, and
the area of the element, and
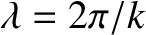 the wavelength. Here,
the wavelength. Here, 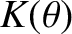 is known as the obliquity factor. Previously (in Section 10.9), we effectively assumed that
is known as the obliquity factor. Previously (in Section 10.9), we effectively assumed that
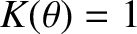 for
for
 , and
, and
 for
for
 . In other words, we assumed that the secondary wave is a half-spherical wave that is emitted isotropically in all forward directions, and
has zero amplitude in all backward directions. In fact, the true obliquity factor is (Jackson 1975)
. In other words, we assumed that the secondary wave is a half-spherical wave that is emitted isotropically in all forward directions, and
has zero amplitude in all backward directions. In fact, the true obliquity factor is (Jackson 1975)
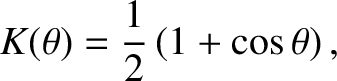
 phase difference between the secondary wave emitted by an element of the aperture, and the light that
illuminates the element from behind. We previously (in Section 10.9) assumed that there was no phase difference.
However, it is easily demonstrated that none of our previous results would be modified had we taken this
phase difference into account.
phase difference between the secondary wave emitted by an element of the aperture, and the light that
illuminates the element from behind. We previously (in Section 10.9) assumed that there was no phase difference.
However, it is easily demonstrated that none of our previous results would be modified had we taken this
phase difference into account.
 , which is such that
, which is such that 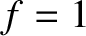 if the
point (
if the
point ( ,
,  , 0) on the opaque screen falls within the aperture, and
, 0) on the opaque screen falls within the aperture, and 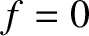 otherwise. It follows
from Equation (10.88) that the wave amplitude at the point (
otherwise. It follows
from Equation (10.88) that the wave amplitude at the point (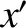 ,
,  ,
,  ) on the projection
screen, which is the resultant of all of the secondary waves that are emitted by the aperture
and travel to this particular point, is given by
) on the projection
screen, which is the resultant of all of the secondary waves that are emitted by the aperture
and travel to this particular point, is given by
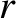
![$\displaystyle =\left[(x-x')^{\,2}+(y-y')^{\,2}+R^{\,2}\right]^{1/2}$](img3555.png)
![$\displaystyle =R + \frac{(x-x')^{\,2}}{2\,R}+ \frac{(y-y')^{\,2}}{2\,R} +{\cal ...
...-x')^{\,4}}{R^{\,3}}\right]
+{\cal O}\left[\frac{(y-y')^{\,4}}{R^{\,3}}\right],$](img3556.png)
![$\displaystyle \cos\theta \equiv \frac{R}{r} = 1-\frac{(x-x')^{\,2}}{2\,R^{\,2}}...
...-x')^{\,4}}{R^{\,4}}\right]
+{\cal O}\left[\frac{(y-y')^{\,4}}{R^{\,4}}\right].$](img3557.png)
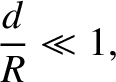
 is the typical aperture dimension (or, to be more exact, the typical value of
is the typical aperture dimension (or, to be more exact, the typical value of 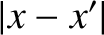 and
and 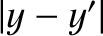 ). In
this limit, Equation (10.90) reduces to
where use has been made of the trigonometric identity
). In
this limit, Equation (10.90) reduces to
where use has been made of the trigonometric identity
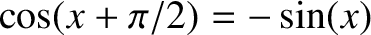 .
The neglect of terms involving
.
The neglect of terms involving
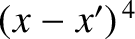 and
and
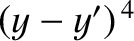 inside the argument of the sine function in the previous equation is
justified provided that
inside the argument of the sine function in the previous equation is
justified provided that
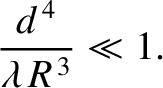
 and
and  , whereas these terms were previously neglected.
Incidentally, far-field diffraction is often referred to as Fraunhofer diffraction, whereas
near-field diffraction is termed Fresnel diffraction.
Note, finally, that because the ordering
, whereas these terms were previously neglected.
Incidentally, far-field diffraction is often referred to as Fraunhofer diffraction, whereas
near-field diffraction is termed Fresnel diffraction.
Note, finally, that because the ordering  implies that
implies that
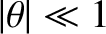 , our previous incorrect assumption for the form of the obliquity factor
makes no difference, because our previous form and the correct form are both characterized by
, our previous incorrect assumption for the form of the obliquity factor
makes no difference, because our previous form and the correct form are both characterized by
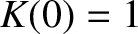 .
.
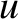
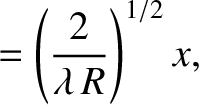
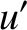
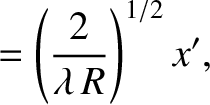

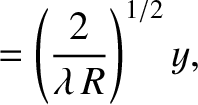
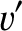
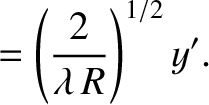
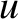 and
and  are dimensionless coordinates that locate a point within the aperture, whereas
are dimensionless coordinates that locate a point within the aperture, whereas
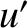 and
and 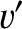 are corresponding coordinates that locate a point on the projection screen.
Equation (10.94) transforms to give
where
are corresponding coordinates that locate a point on the projection screen.
Equation (10.94) transforms to give
where
 for all
for all 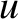 and
and  .
In this case, the two-dimensional integrals in the previous two equations become separable. Making use of some standard trigonometric identities (see Section B.3), we obtain
.
In this case, the two-dimensional integrals in the previous two equations become separable. Making use of some standard trigonometric identities (see Section B.3), we obtain
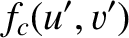
![$\displaystyle = \frac{1}{2}\left[\int_{-\infty}^\infty \cos\left(\frac{\pi}{2}\...
...t[\int_{-\infty}^\infty \sin\left(\frac{\pi}{2}\,t^{\,2}\right)dt\right]^{\,2},$](img3587.png)
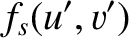
![$\displaystyle =\left[\int_{-\infty}^\infty \cos\left(\frac{\pi}{2}\,t^{\,2}\rig...
...t]\left[\int_{-\infty}^\infty \sin\left(\frac{\pi}{2}\,t^{\,2}\right)dt\right].$](img3588.png)
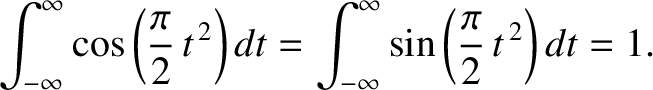
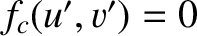 and
and
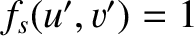 , which, from Equation (10.102), implies that
, which, from Equation (10.102), implies that
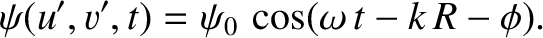
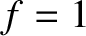 everywhere) then the incident wave,
everywhere) then the incident wave,
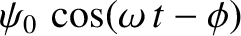 , illuminating the aperture from behind, propagates in the
, illuminating the aperture from behind, propagates in the  -direction without changing amplitude, and acquires a phase shift
-direction without changing amplitude, and acquires a phase shift 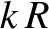 by the time
it reaches the projection screen. The previous result is the ultimate justification for the
Hugyens–Fresnel formula, (10.88).
by the time
it reaches the projection screen. The previous result is the ultimate justification for the
Hugyens–Fresnel formula, (10.88).

 denotes an average over a wave period.
It follows from Equation (10.102) that
where
denotes an average over a wave period.
It follows from Equation (10.102) that
where
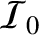 is the illumination intensity when the aperture is completely transparent.
Here, use has been made of the standard results
is the illumination intensity when the aperture is completely transparent.
Here, use has been made of the standard results
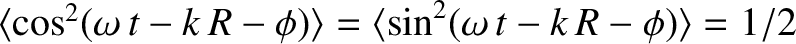 and
and
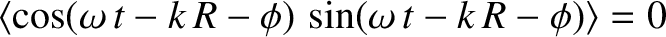 .
.